Формы представления Графов затрат
Автор: Александр Поляков
Смотреть видео: 1.Графы затрат. Вводная часть
Как известно, графом называют абстрактный комбинаторный математический объект, представляющий собой множество узлов (вершин) и множество пар узлов, называемых ребрами. Если порядок расположения узлов в парах не имеет значения, т.е. на ребрах не задано направление, то такой граф называется неориентированным. Если узлы в паре упорядочены, т.е. задано направление на ребрах, то такие ребра называют дугами, а граф называют ориентированным графом или орграфом.
Граф является математической (чистой) структурой и ее нельзя наблюдать непосредственно в эмпирической реальности, ее можно только мысленно представлять, как и любую другую чистую структуру, например, множество натуральных чисел. Графы, как математические структуры, очень удобны и в настоящее время довольно часто применяются при построении теорий в различных предметных областях. В нашем случае мы используем орграфы для моделирования движений потоков стоимостей и, в частности, потоков затрат на предприятии. В результате мы получаем модели в виде Графов предприятий и их подграфов – Графов затрат.
Для описания бухгалтерской реальности мы используем Граф предприятия, состоящий из множества счетов учета Ai (узлов) и множества корреспонденций счетов учета, представляющих собой упорядоченные пары корреспондирующих счетов учета (Ai,Aj), первый из которых Ai корреспондирует по кредиту, а второй счет учета Aj – по дебету. В Графе затрат (подграфе Графа предприятия) для узлов используется специальное название – центры затрат.
Как правило, множество корреспонденций счетов учета в отчетном периоде достаточно велико, поэтому существует необходимость представления этих операций в удобной для дальнейшего анализа форме. При этом следует помнить, что, выбирая какую-либо форму представления орграфа, мы не изменяем сам орграф, а просто представляем его в наиболее удобном для решения задачи виде.
В данной статье мы рассмотрим три наиболее часто используемые формы представления графов и орграфов – табличную (ее еще называют матричной), геометрическую (ее еще называют графической), а также форму представления с помощью множеств. Не изменяя граф или орграф, как математический объект, каждая форма представления, тем не менее, предполагает собственный подход к формированию терминологии теории графов.
Например, ниже на рисунке показаны три формы представления орграфа G(5,7):
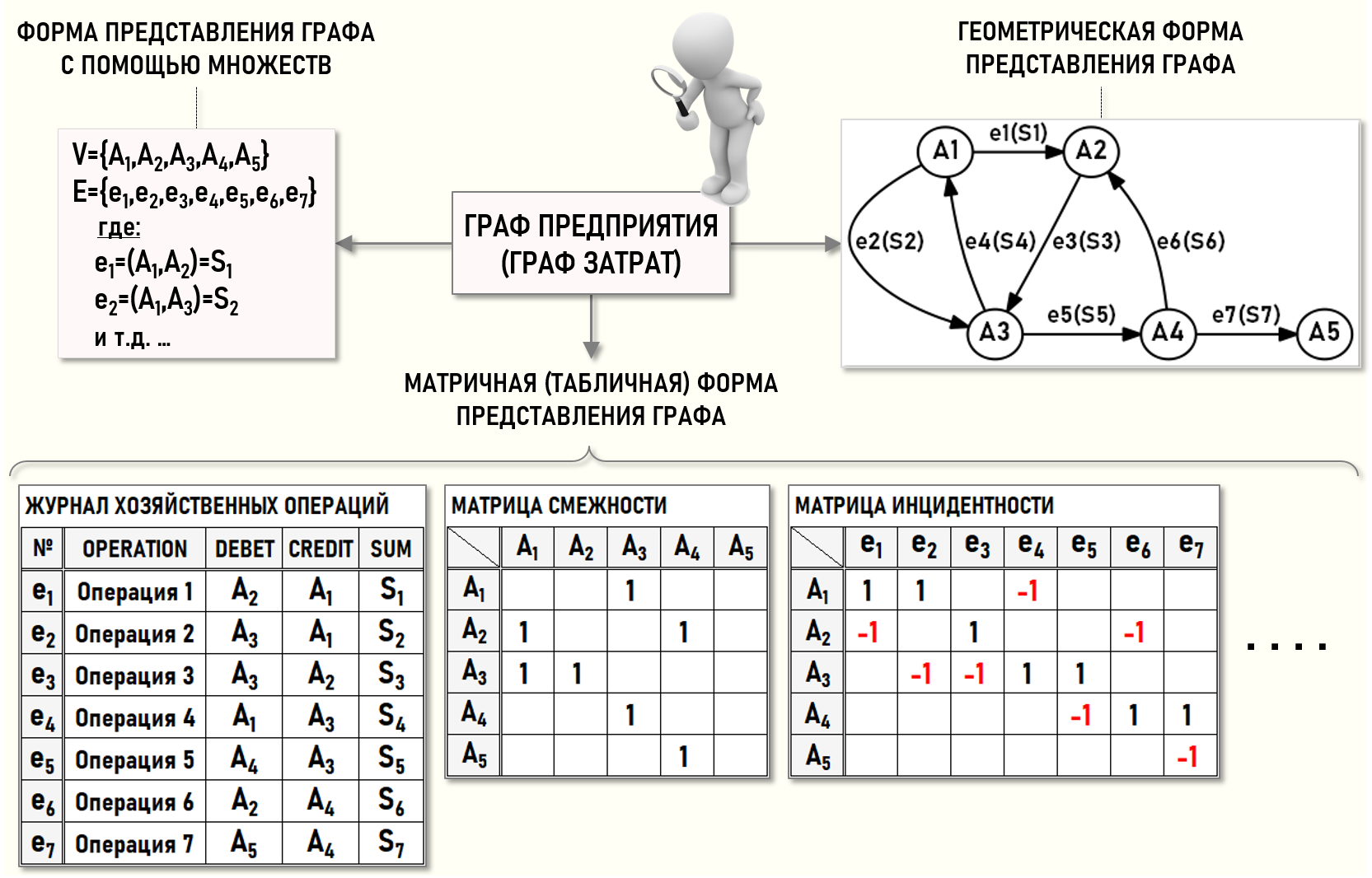
Геометрическая (графическая) форма
Данная форма представления графов предполагает, что графом называется геометрическая фигура, состоящая из узлов и отрезков, соединяющих узлы между собой. Отрезки могут быть прямолинейными или криволинейными, а также направленными – и тогда они называются дугами, и ненаправленными – такие отрезки называются ребрами. Далее мы будем иметь дело в основном с дугами, а значит с орграфами.
Также необходимо отметить, что представленный в геометрической форме орграф можно рассматривать скорее не как геометрическую, а как топологическую фигуру, поскольку заключенная в нем информация о хозяйственной деятельности предприятия не зависит от расположения узлов орграфа на плоскости или в трехмерном пространстве, а также от того, какие дуги их соединяют – прямолинейные или криволинейные. Один и тот же орграф можно изобразить по-разному, это всего лишь вопрос удобства работы с ним.
В практической деятельности часто именно с геометрической формой представления отождествляют само понятие графа или орграфа. Однако следует помнить, что это только один из возможных вариантов представления, хотя и наиболее наглядный, и привычный многим учетным специалистам.
Форма представления с помощью множеств
При выборе данной формы представления предполагается, что орграфом называется пара множеств (A,E), где:
A – множество узлов орграфа (счетов учета или центров затрат)
E – множество дуг орграфа (корреспонденций счетов учета или центров затрат)
Каждая дуга орграфа может характеризоваться уникальным идентификатором (en), также ее можно представить упорядоченной парой узлов (Ai,Aj), в которой первый узел Ai обозначает начало дуги, а второй узел Aj– ее окончание.
Например:
e1=(A1,A2)=S1
где:
e1 – уникальный идентификатор дуги
A1 – узел, в котором дуга начинается (кредит счета или центра затрат)
A2 – узел, в котором дуга заканчивается (дебет счета учета или центра затрат)
S1 – вес дуги (сумма операции)
Матричная (табличная) форма
Данная форма представления орграфов выбирается тогда, когда для решения задачи имеется необходимость представить узлы и дуги орграфа с помощью таких матриц, как, например – матрица смежности, матрица инцидентности и т.п., а также с помощью специальных матриц, применяемых для решения задач на Графах затрат – матрица исходных коэффициентов, матрица коэффициентов уравнений, матрица стоимостей и т.п. Такой таблицей в том числе является и журнал хозяйственных операций (ЖХО).
Довольно часто от учетных специалистов можно услышать вопрос – как можно построить орграф на основе первичных учетных данных из ЖХО? Ответ очевиден.
Во-первых, ЖХО представляет собой таблицу, в которой уже содержится вся информация об узлах и дугах Графа предприятия (Графа затрат), т.е. данный орграф уже представлен в ЖХО в табличной форме.
Во-вторых, это не мешает представить орграф еще и в геометрической форме, т.е. в виде рисунка. В этом случае в ЖХО и на рисунке будет представлен один и тот же орграф, содержащий одну и ту же информацию о хозяйственных операциях предприятия, просто этот орграф будет представлен с помощью разных форм.
Несмотря на то, что геометрическая (графическая) форма представления орграфов считается наиболее привычной, и многие учетные специалисты часто вообще ассоциируют с орграфами только их графические представления, тем не менее некоторым учетным специалистам на первых порах бывает сложно «разглядеть» орграфы в своих учетных моделях. Например, ниже на рисунке показана модель в виде бухгалтерских «самолетиков».
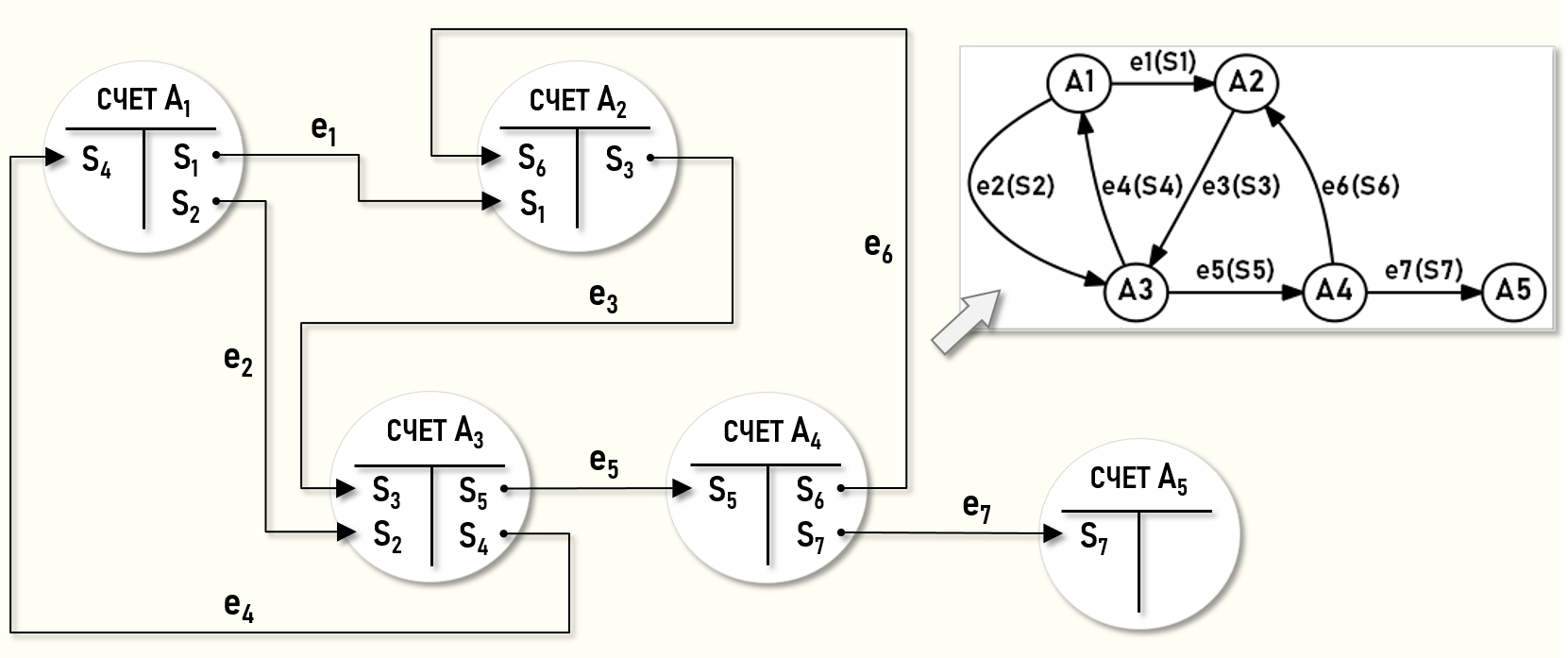
Подобное представление операций двойной записи уже давно используется учетными специалистами, но не всем из них приходит в голову рассматривать счета учета в качестве узлов орграфа, а корреспонденции счетов учета в качестве его дуг, хотя это довольно очевидно.
Выше мы уже отмечали, что Граф предприятия и Граф затрат скорее можно рассматривать не как геометрические, а как топологические фигуры. Это значит, что информация о движении потоков стоимостей через цепочки узлов не зависит от особенностей их взаимного расположения на плоскости или в трехмерном пространстве. Также не имеет значения, какие виды дуг соединяют узлы – прямолинейные или криволинейные, поскольку это влияет только на удобство восприятия нарисованного орграфа.
Ниже на рисунке представлены три варианта расположения на плоскости одного и того же Графа предприятия. Несмотря на то, что схемы расположения на плоскости узлов и дуг в каждом из вариантов различны, перед нами один и тот же орграф, т.е. все варианты содержат одинаковую информацию о движении потоков стоимостей на рассматриваемом предприятии.
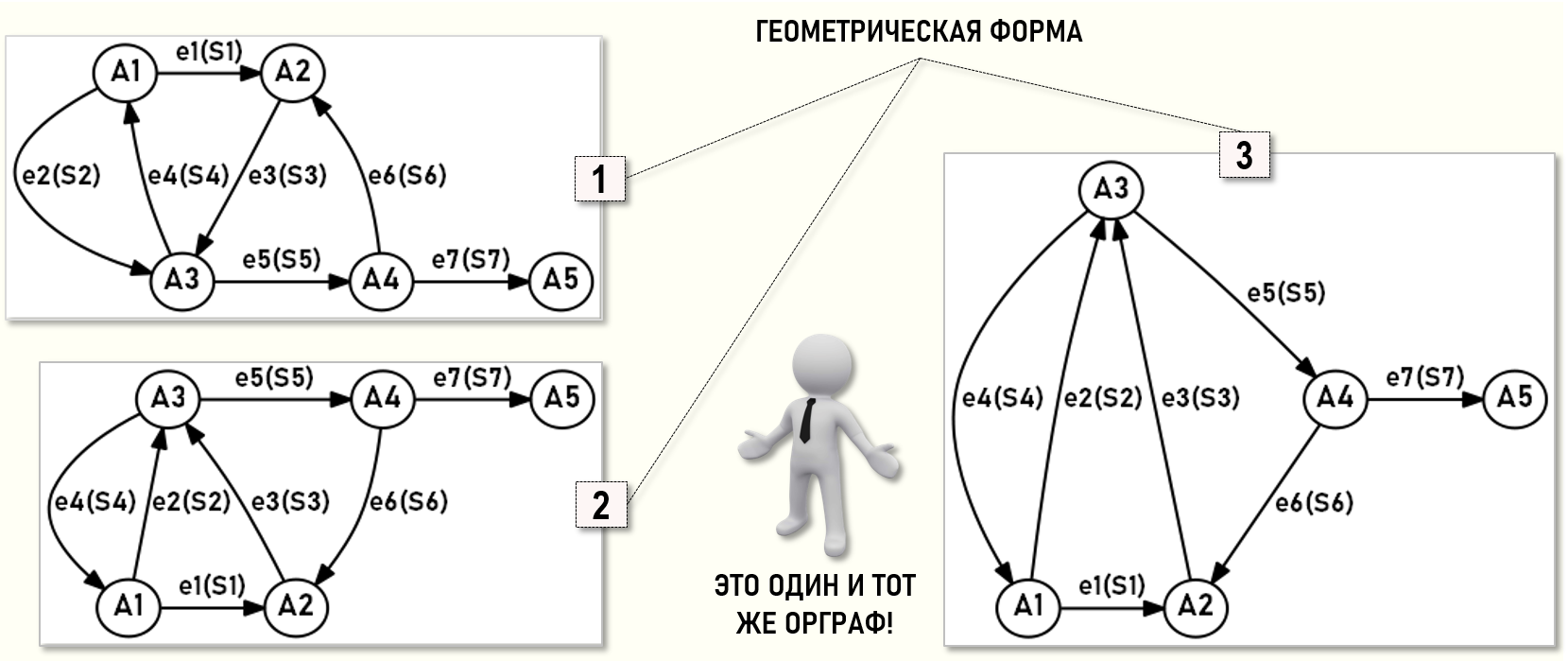
Изучая Графы предприятий и их подграфы – Графы затрат мы будем далее использовать все формы их представления, выбирая в каждом конкретном случае ту из них, которая наиболее подходит к существу рассматриваемого вопроса.
Еще раз зафиксируем внимание читателя на том, что любой Граф предприятия и Граф затрат может быть представлен с помощью рисунка, таблицы (матрицы) или перечисления элементов множества узлов и дуг. Выбранная форма представления всего лишь помогает учетным специалистам работать с орграфом в том виде, который является наиболее удобным для решения конкретной задачи.

