Расчет себестоимости (СЛАУ). Элементы затрат (ч.1)

   

Автор:  Александр Поляков

    

В первой и во второй части предыдущей статьи мы подробно рассмотрели два варианта процедуры расчета себестоимости предприятия, основанной на решении СЛАУ, использовав для этого типовой функционал Microsoft Excel. В данной статье мы усложним условия задачи и рассчитаем себестоимость для случая, когда требуется определить ее структуру в разрезе элементов затрат. Рекомендуется скачать таблицы Microsoft Excel для рассматриваемого примера и работать с ними в процессе изучения материала статьи.

В статье (также состоящей из двух частей) будут рассмотрены два варианта группировки затрат по элементам затрат. В первой части будет решена задача расчета себестоимости в разрезе общеизвестных элементов затрат – материальные затраты, амортизация, затраты на оплату труда, прочие затраты. В учебных целях мы рассмотрим пример расчета только для двух элементов затрат из этой группы – для материальных затрат и затрат на оплату труда, поскольку процедура расчета себестоимости для каждого элемента затрат является однотипной. В данном случае принципиально важно, что элементов затрат больше, чем один, а увеличение числа элементов затрат приведет просто к масштабированию модели.

Во второй части статьи будет произведен расчет себестоимости для случая, когда группировка тех же самых(!) затрат предприятия происходит по другому принципу – все затраты делятся на затраты по договору №1 и прочие затраты. К затратам по договору №1 будут отнесены все затраты предприятия, связанные с выполнением договора №1, а все остальные затраты предприятия будут объединены в другой элемент затрат – прочие затраты.

Таким образом, в обеих частях статьи будет рассчитана себестоимость для одного и того же предприятия в одном и том же отчетном периоде, но для целей подготовки различных управленческих решений будут получены разные структуры себестоимости – в разрезе двух различных групп элементов затрат. Понятно также, что, выделив какие-либо другие группы элементов затрат, можно будет получить и другие структуры себестоимости, поскольку процедура расчета себестоимости будет аналогична той, что мы рассмотрим в данной статье.

  

ЧАСТЬ 1. МАТЕРИАЛЬНЫЕ ЗАТРАТЫ И ЗАТРАТЫ НА ОПЛАТУ ТРУДА

  

Условия задачи. Элементы первичных затрат

Матричная форма СЛАУ для элементов затрат

Решение СЛАУ для элементов затрат

Матрицы стоимостей для элементов затрат

  

 УСЛОВИЯ ЗАДАЧИ. ЭЛЕМЕНТЫ ПЕРВИЧНЫХ ЗАТРАТ  (↑)

  

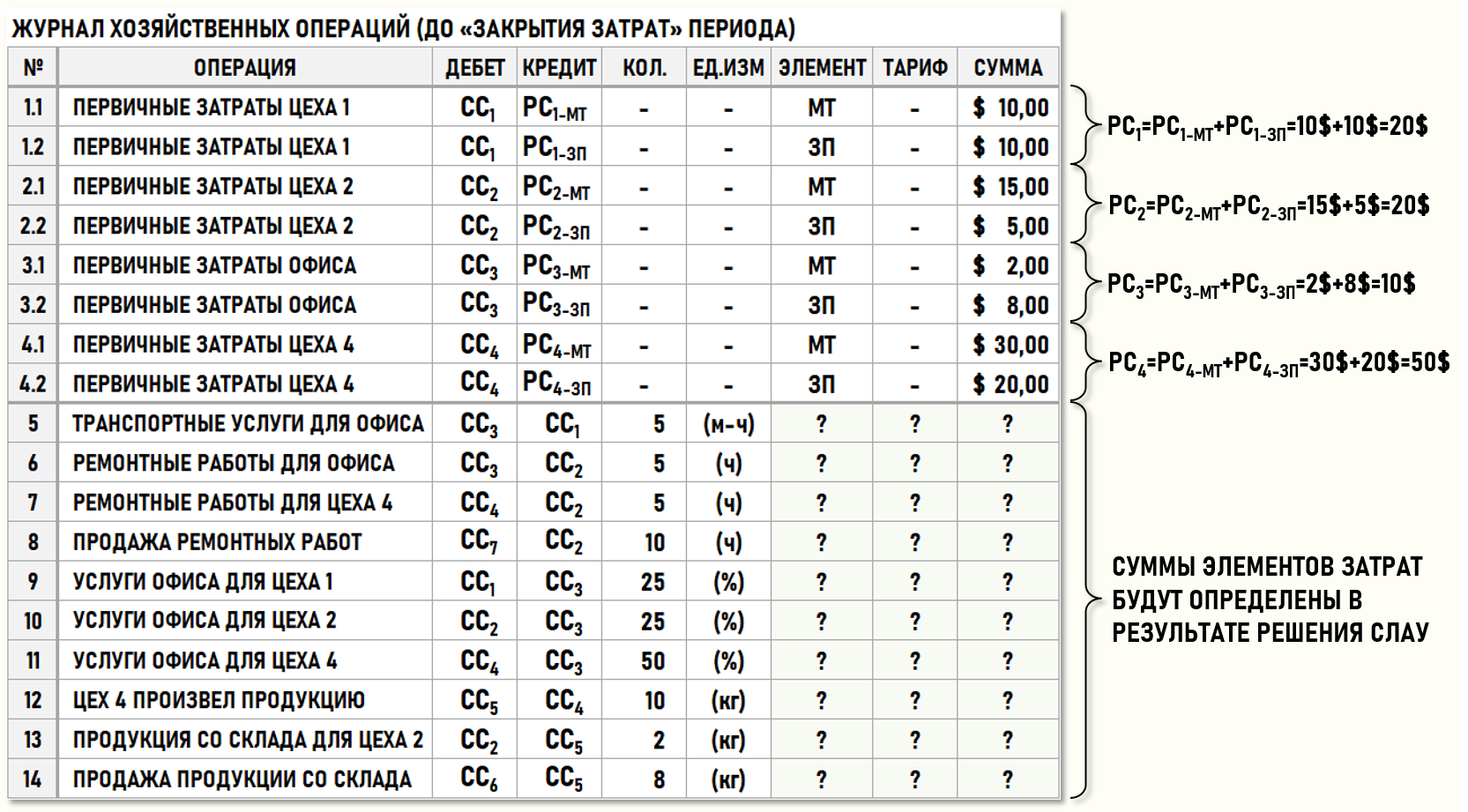
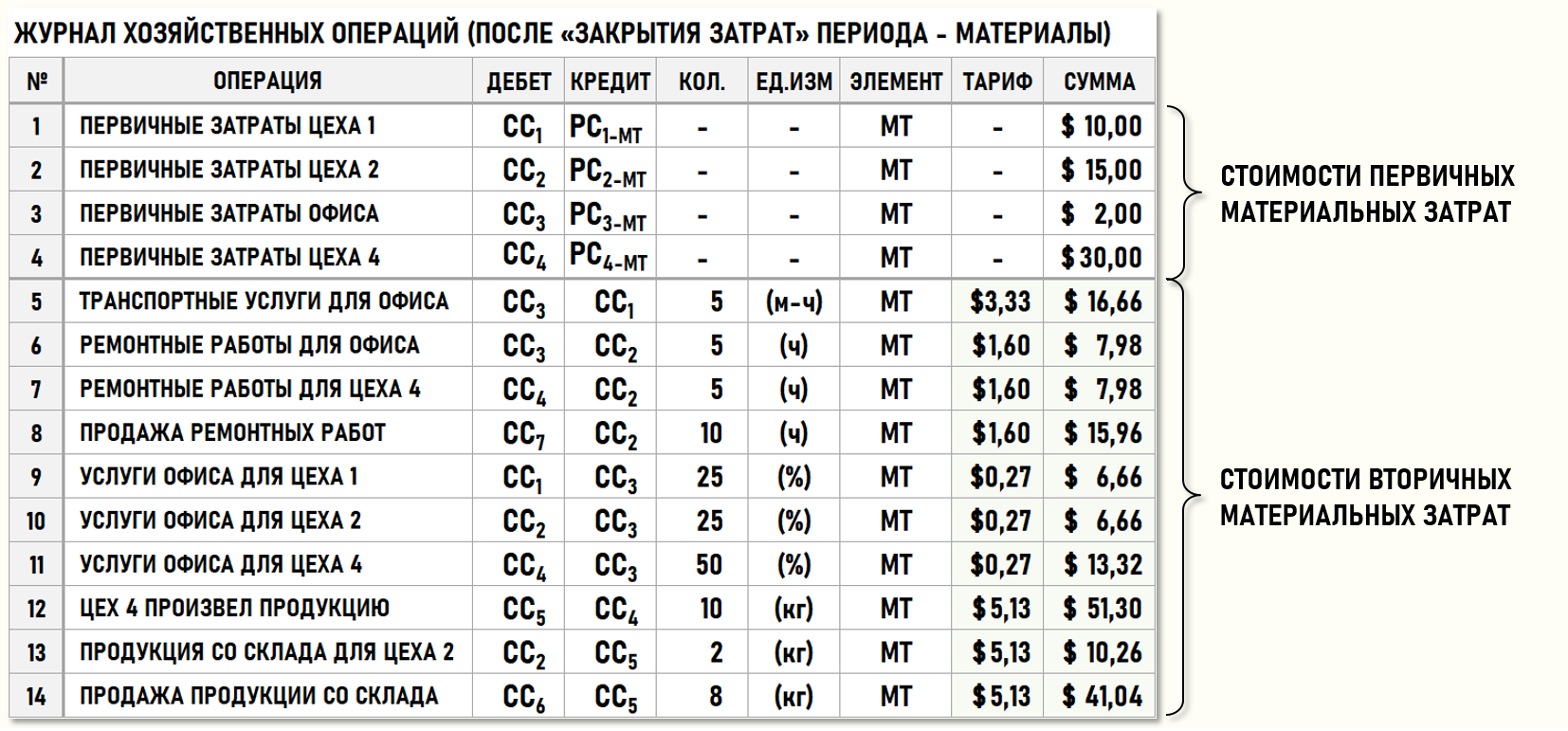
Предприятие производит и продает продукцию, а также выполняет (продает) для сторонних контрагентов ремонтные работы. Ниже на рисунке представлен журнал хозяйственных операций (ЖХО) предприятия за отчетный период.

   

     

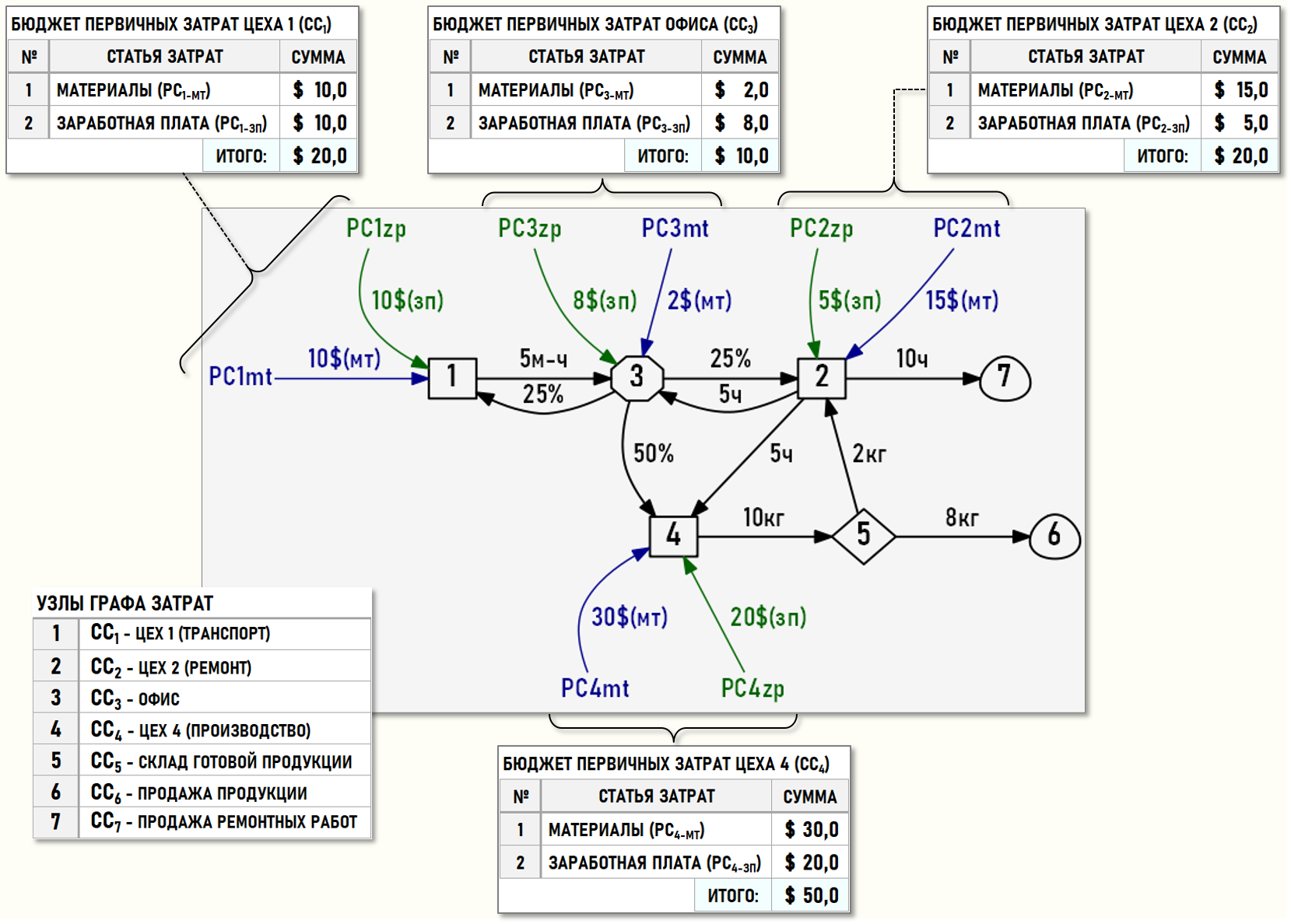
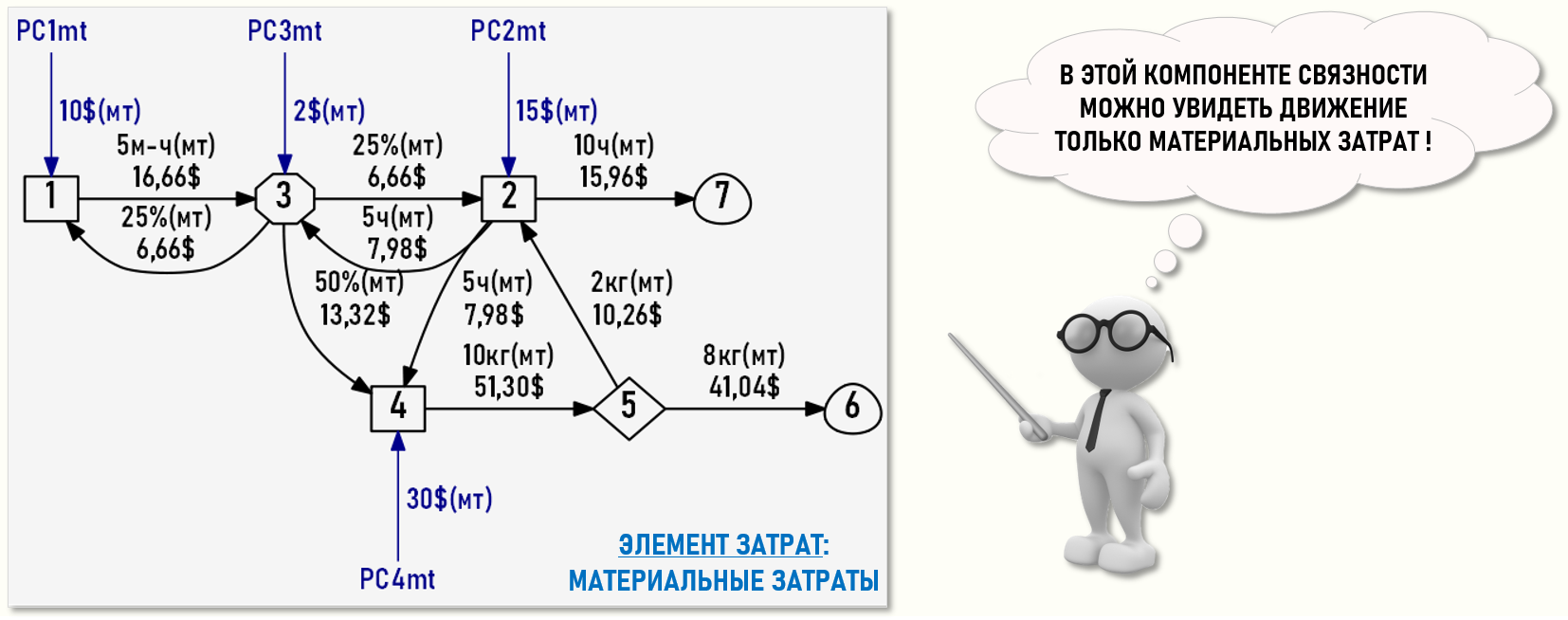
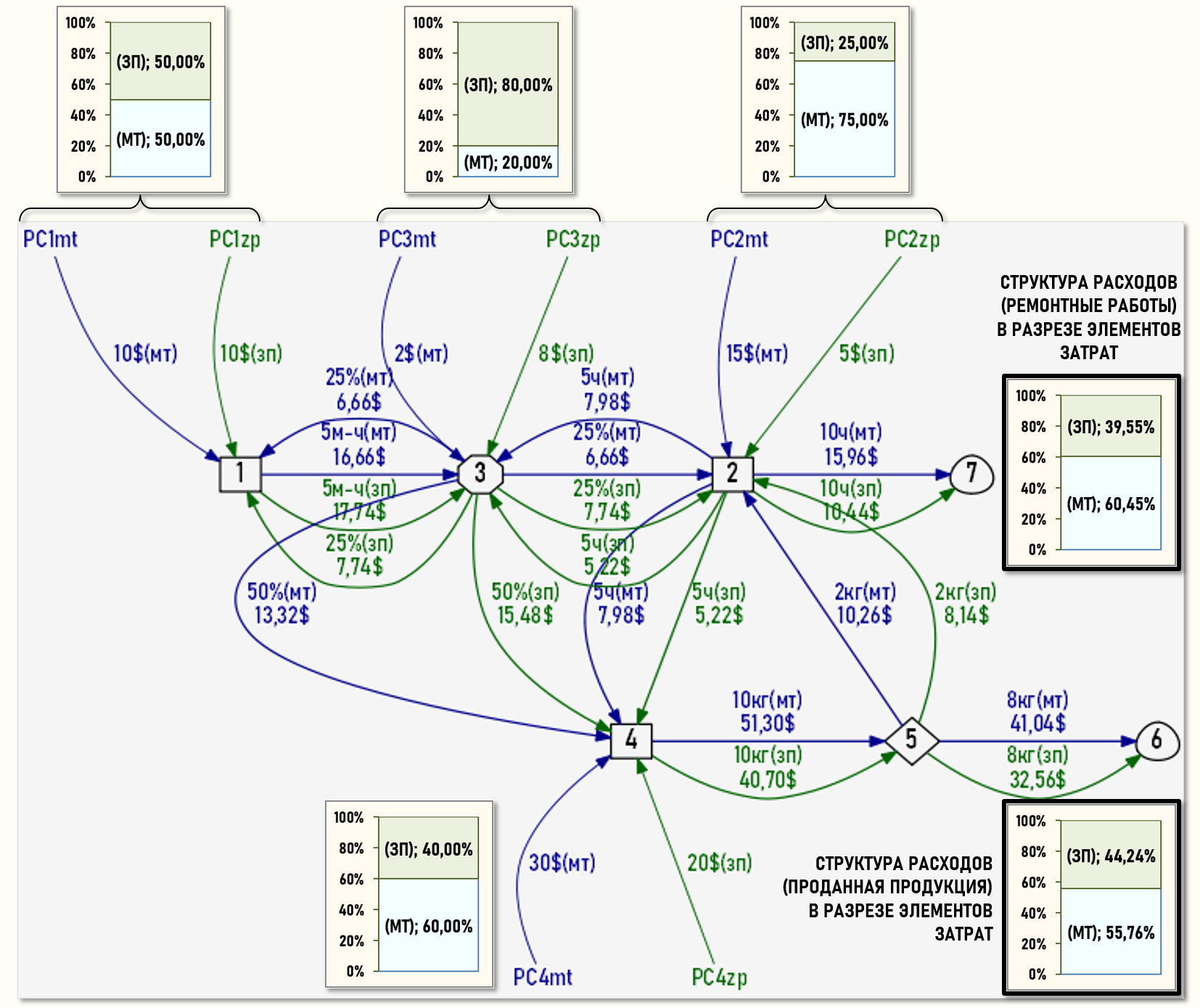
Также представим множество хозяйственных операций в виде рисунка – Графа затрат, весами дуг которого являются количества единиц калькуляции и стоимости элементов затрат. На рисунке также представлены бюджеты первичных затрат для цехов и офиса предприятия. В строках данных бюджетов содержатся стоимости первичных материальных затрат и суммы заработной платы для каждого подразделения предприятия.

   

 

В предыдущей статье мы решили данную задачу для общих стоимостей затрат, предполагая, что структура затрат в разрезе элементов затрат пользователя не интересует. Теперь же пользователя модели интересует информация о структуре себестоимости проданной продукции и проданных ремонтных работ в разрезе двух элементов затрат – материальные затраты (мт) и затраты на оплату труда (зп).

Напомним, что все затраты предприятия можно разделить на два класса – первичные затраты и вторичные затраты. Стоимость первичных затрат всегда известна до начала выполнения процедуры закрытия затрат периода, стоимость вторичных затрат можно определить только по результатам проведения процедуры закрытия затрат периода.

Первый шаг процедуры расчета себестоимости в разрезе элементов затрат состоит в том, чтобы разделить по элементам затрат все первичные затраты предприятия, что и было сделано с помощью соответствующих бюджетов первичных затрат. Понятно, что элементы первичных затрат не должны «пересекаться» между собой, т.е. не должно быть первичных затрат, входящих одновременно в обе группы.

Цех 1 (СС₁) оказал транспортные услуги Офису (СС₃) в количестве 5-ти машино-часов. Общие стоимости первичных затрат (20$) Цеха 1 складываются из стоимости использованных материалов (10$) и начисленной сотрудникам цеха заработной платы (10$).

Цех 2 (СС₂) выполнил ремонтные работы для Офиса (СС₃) и для Цеха 4 (СС₄) в количестве 5-ти часов каждому, а также для сторонних контрагентов в количестве 10-ти часов (продал ремонтные работы). Себестоимость проданных ремонтных работ формируется на входе центра затрат СС₇. Общие стоимости первичных затрат (20$) Цеха 2 складываются из стоимости использованных материалов (15$) и начисленной сотрудникам цеха заработной платы (5$).

Цех 4 (СС₄) произвел в отчетном периоде 10 килограммов продукции и поместил ее на склад предприятия (СС₅). Часть продукции со склада (8кг) была продана покупателям, а оставшаяся продукция (2кг) в этом же периоде была использована Цехом 2 (СС₂) для производства ремонтных работ. Себестоимость проданной продукции формируется на входе центра затрат СС₆. Общие стоимости первичных затрат (50$) Цеха 4 складываются из стоимости использованных материалов (30$) и начисленной сотрудникам цеха заработной платы (20$).

Управление деятельностью предприятия производится административным персоналом в Офисе (СС₃). Распределение стоимости управленческих затрат Офиса (СС₃) производится в следующих пропорциях – по 25% получают Цех 1 (СС₁) и Цех 2 (СС₂), а оставшиеся 50% приходятся на долю Цеха 4 (СС₄). В данном случае рассчитываются полные себестоимости проданных продукции и ремонтных работ, поскольку в них включаются и стоимости затрат на управление предприятием. Общие стоимости первичных затрат (10$) Офиса складываются из стоимости использованных материалов (2$) и начисленной административному персоналу заработной платы (8$).

Первые восемь записей ЖХО (с 1.1 по 4.2) содержат общие стоимости элементов первичных затрат, полученных цехами и офисом предприятия в рассматриваемом периоде. Пока не будет выполнена процедура закрытия затрат периода, только эти записи характеризуются не 0-выми стоимостями.

Записи ЖХО с 5-ой по 14-ю содержат пока только общие количества единиц калькуляции за весь рассматриваемый период. Эти значения всегда известны до начала процедуры закрытия затрат периода. Стоимости элементов затрат для этих хозяйственных операций будут определены по результатам проведения процедуры закрытия затрат периода.

 

МАТРИЧНАЯ ФОРМА СЛАУ ДЛЯ ЭЛЕМЕНТОВ ЗАТРАТ  (↑)       

 

Когда не ставилась задача расчета себестоимости в разрезе элементов затрат, СЛАУ в матричной форме имела следующий вид:

P[7,7] T_UC[7] = Z[7]

где:

P[7,7] – матрица коэффициентов уравнений

T_UC[7] – вектор-столбец тарифов

Z[8] – вектор-столбец правых частей уравнений

Теперь же необходимо рассчитать себестоимость отдельно для каждого из двух элементов затрат, поэтому одной СЛАУ уже недостаточно, для каждого элемента затрат необходимо сформировать свою СЛАУ.

   

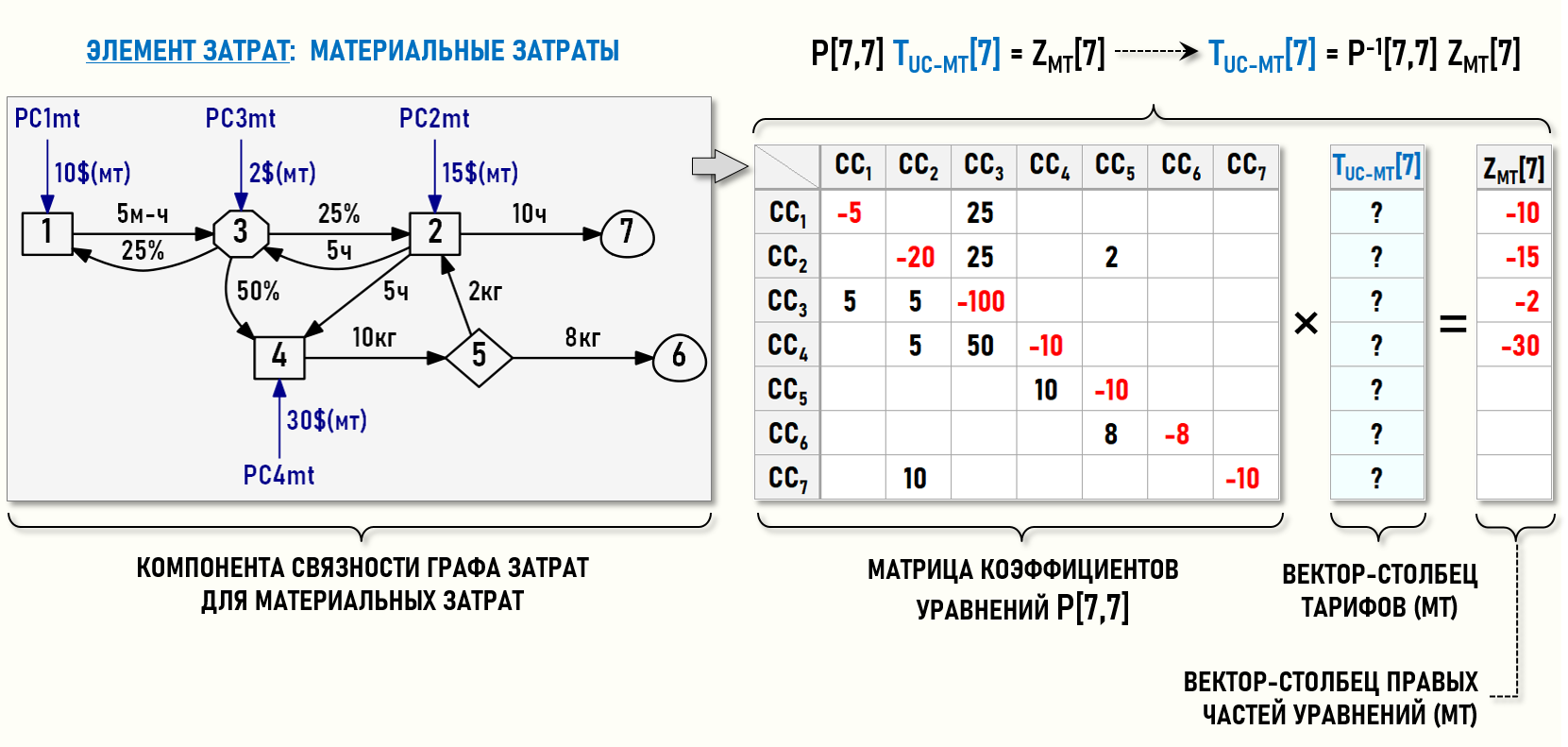
СЛАУ для материальных затрат:

P[7,7] T_UC-МТ[7] = Z_МТ[7]

где:

P[7,7] – матрица коэффициентов уравнений

T_UC-МТ[7] – вектор-столбец тарифов для материальных затрат

Z_МТ[7] – вектор-столбец правых частей уравнений для материальных затрат

  

   

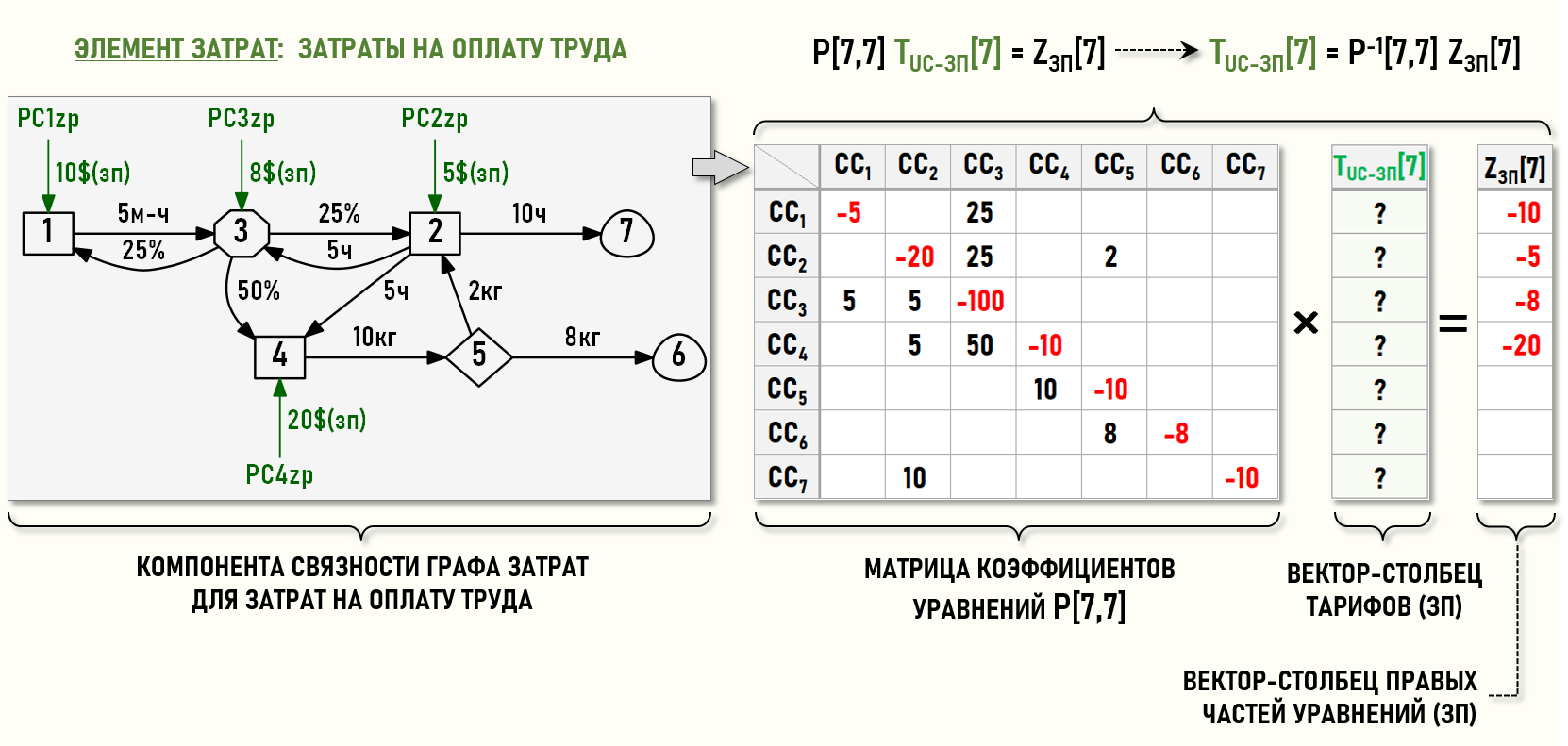
СЛАУ для затрат на оплату труда:

P[7,7] T_UC-ЗП[7] = Z_ЗП[7]

где:

P[7,7] – матрица коэффициентов уравнений

T_UC-ЗП[7] – вектор-столбец тарифов для затрат на оплату труда

Z_ЗП[7] – вектор-столбец правых частей уравнений для затрат на оплату труда

   

 

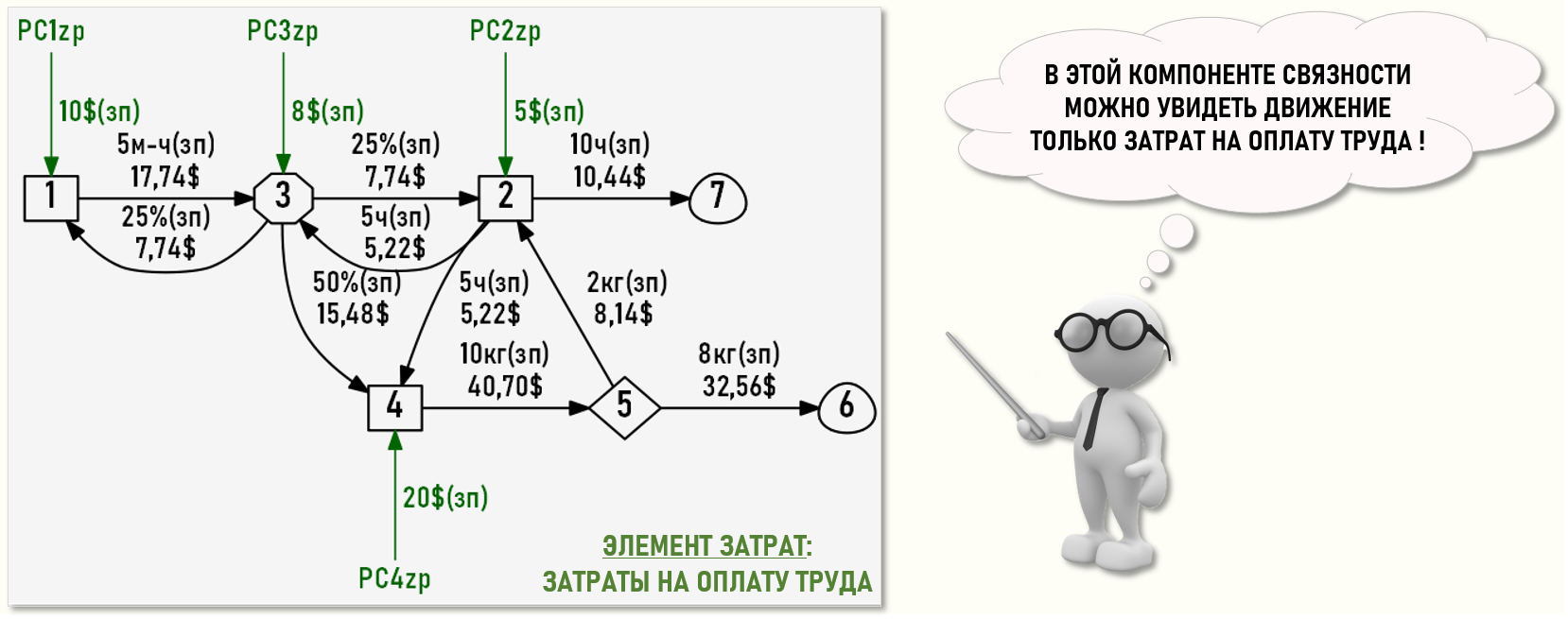
Использование элементов затрат предполагает разделение «общего» Графа затрат на компоненты связности, т.е. несвязанные между собой подграфы, соответствующие отдельным элементам затрат. В нашем примере мы фактически получили два отдельных подграфа – компоненты связности отдельно для каждого элемента затрат, в которых можно посмотреть, как ведут себя только материальные затраты и только затраты на оплату труда.

Матрица коэффициентов уравнений P[7,7] одинакова для обеих СЛАУ, т.к. она содержит только количественные характеристики потоков вторичных затрат – количества продукции, работ и услуг, которыми обменялись центры затрат в течение отчетного периода, а это количество не зависит от того, какие элементы затрат используются при расчете себестоимости. Остальные матрицы необходимо формировать для каждого элемента затрат в отдельности.

Целью закрытия затрат периода в разрезе элементов затрат является определение тарифов, т.е. стоимостей единиц калькуляции для каждого элемента затрат в отдельности. В нашем случае на выходе каждого центра затрат теперь надо искать два тарифа – для материальных затрат и для затрат на оплату труда, что позволит определить, какая часть общего тарифа определяется стоимостью материальных затрат, а какая часть – стоимостью затрат на оплату труда. Другими словами, необходимо определить структуру тарифа в разрезе элементов затрат.

Поскольку при движении по Графу затрат потоки разных элементов затрат не пересекаются между собой (как электрический ток в проводах), т.е. никакие затраты предприятия не могут входить одновременно в группу материальных затрат и затрат на оплату труда, то закрытие затрат периода можно проводить для каждого элемента затрат в отдельности – отдельно закрываются затраты периода только для материальных затрат и отдельно закрываются затраты только для затрат на оплату труда.

В статье рассматривается процедура решения СЛАУ с помощью стандартного функционала Microsoft Excel. Используется вариант, основанный на понижении размерности задачи. Целью решения обеих СЛАУ является определение вектора-столбца тарифов для соответствующего элемента затрат:

T_UC-МТ[7] = P^-1[7,7] Z_МТ[7]

T_UC-ЗП[7] = P^-1[7,7] Z_ЗП[7]

где:

P^-1[7,7] – обратная матрица коэффициентов уравнений

    

РЕШЕНИЕ СЛАУ ДЛЯ ЭЛЕМЕНТОВ ЗАТРАТ  (↑)

  

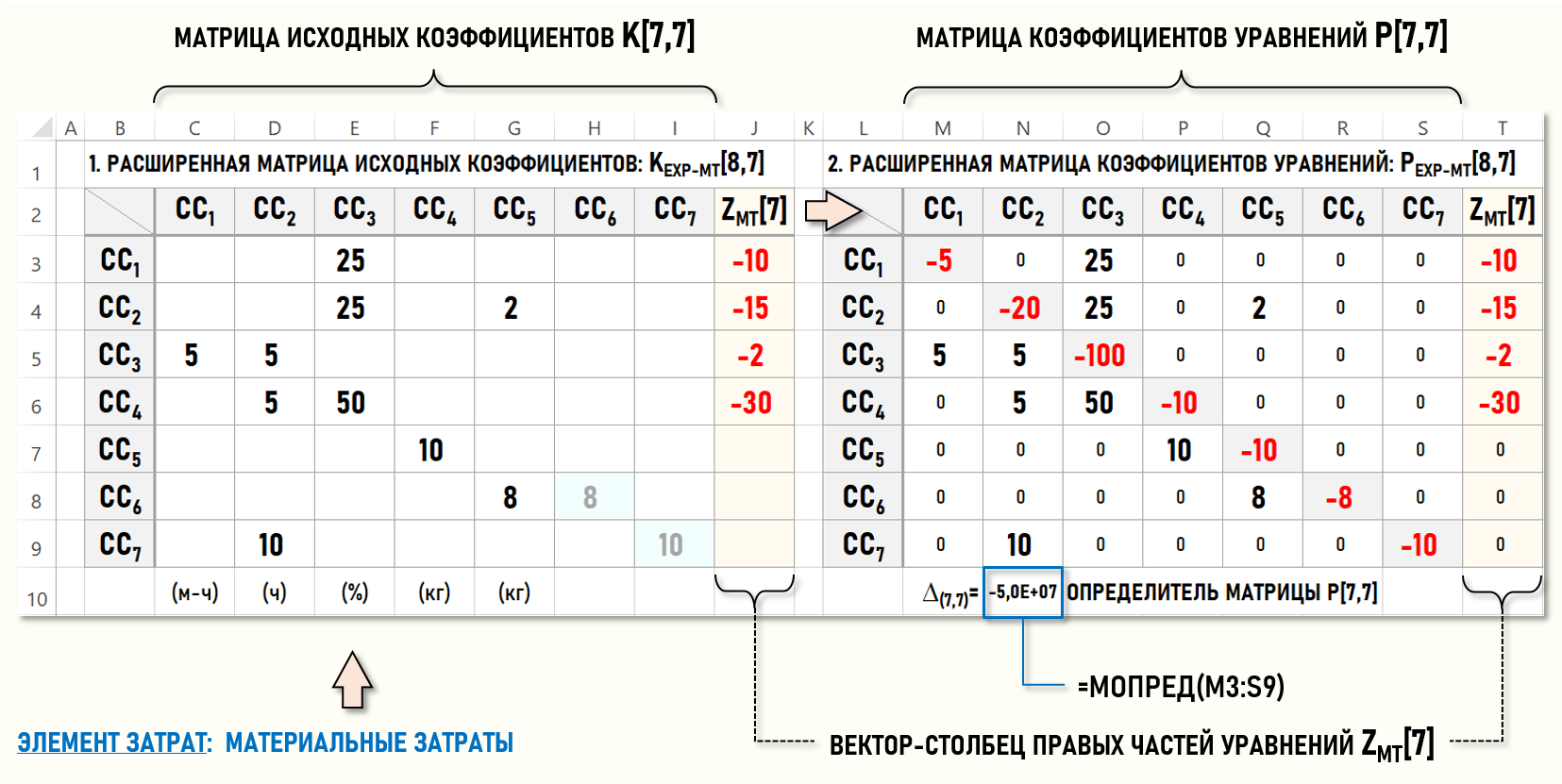
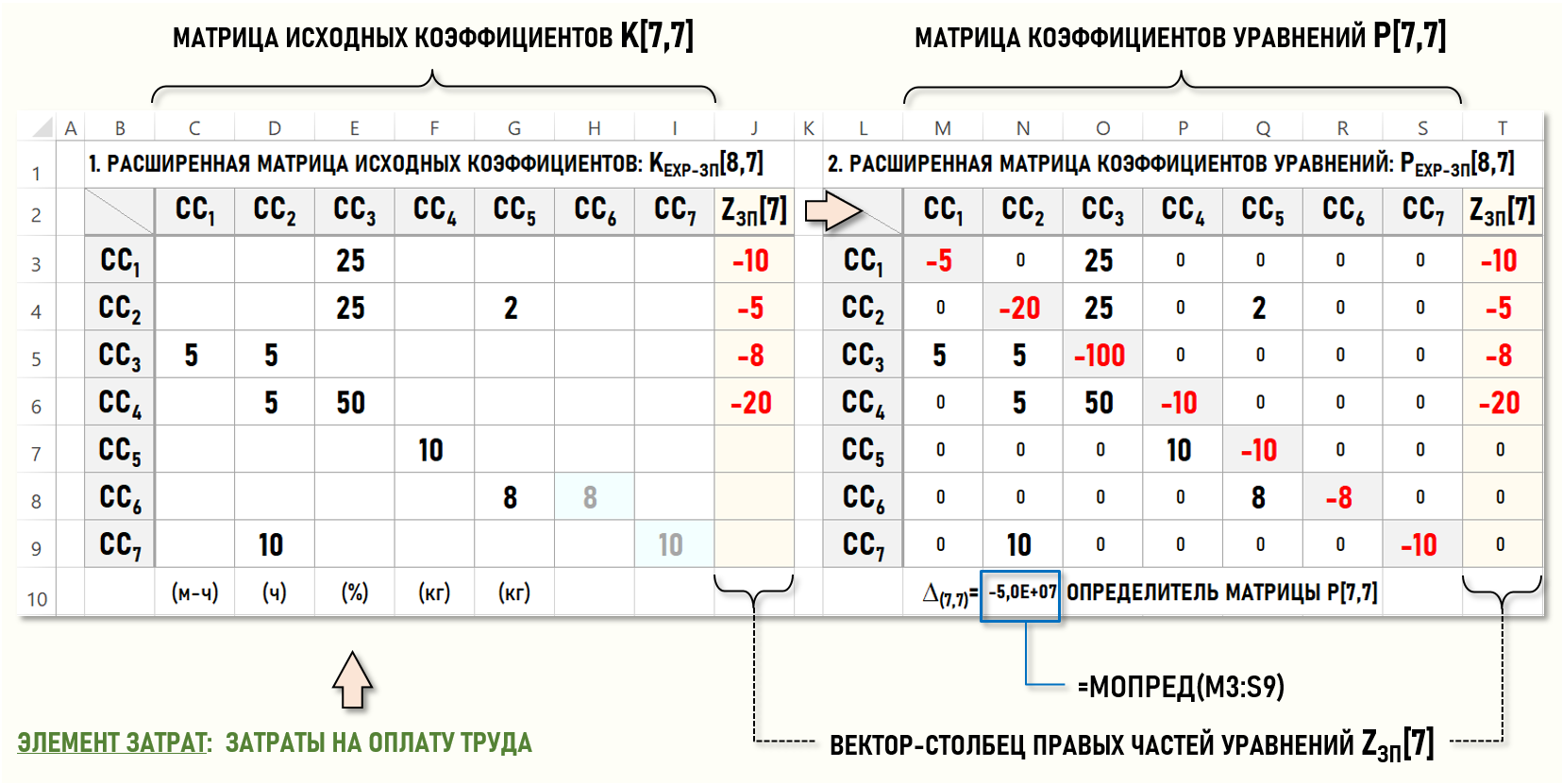
Представим СЛАУ для элементов затрат с помощью расширенных матриц коэффициентов уравнений P_EXP-МТ[8,7] и P_EXP-ЗП[8,7]. Технологические особенности работы с таблицами Microsoft Excel предполагают, что все пустые ячейки этих матриц необходимо заполнить 0-ми.

   

 

   

   

На рисунках также показаны расширенные матрицы исходных коэффициентов для каждого элемента затрат – K_EXP-МТ[8,7] и K_EXP-ЗП[8,7], которые не присутствуют в явном виде в СЛАУ, но более удобны для практической работы, т.к. позволяют в наглядной и компактной форме представить всю необходимую для распределения вторичных затрат информацию.

Как уже говорилось в предыдущей статье, при использовании варианта расчета себестоимости, основанного на уменьшении размерности СЛАУ, часто не заполняют диагональные элементы матриц для стоков, в которых формируются расходы предприятия, поскольку далее в расчетах они не учитываются и уменьшают наглядность матриц. Выше на рисунках количества проданных продукции и ремонтных работ показаны два раза, один раз в столбцах для CC₂ и CC₅, и второй раз – в столбцах для CC₆ и CC₇, что можно считать избыточным для пользователя модели.

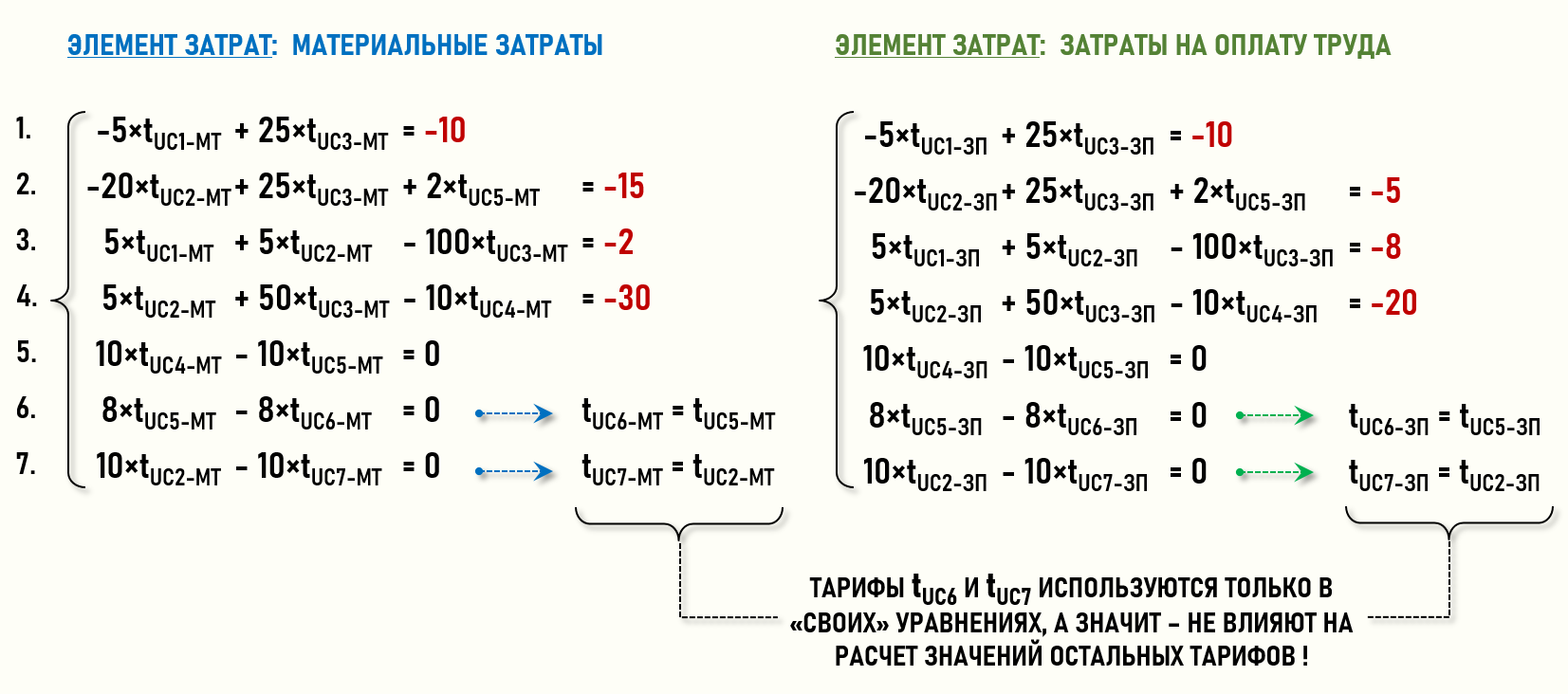
Представив СЛАУ в «обычной» форме, можно увидеть, что уравнения 6 и 7 фактически не нужны, т.к. тарифы t_UC6 и t_UC7 используются только в «своих» уравнениях, а значит – не влияют на расчет значений остальных тарифов.

  

 

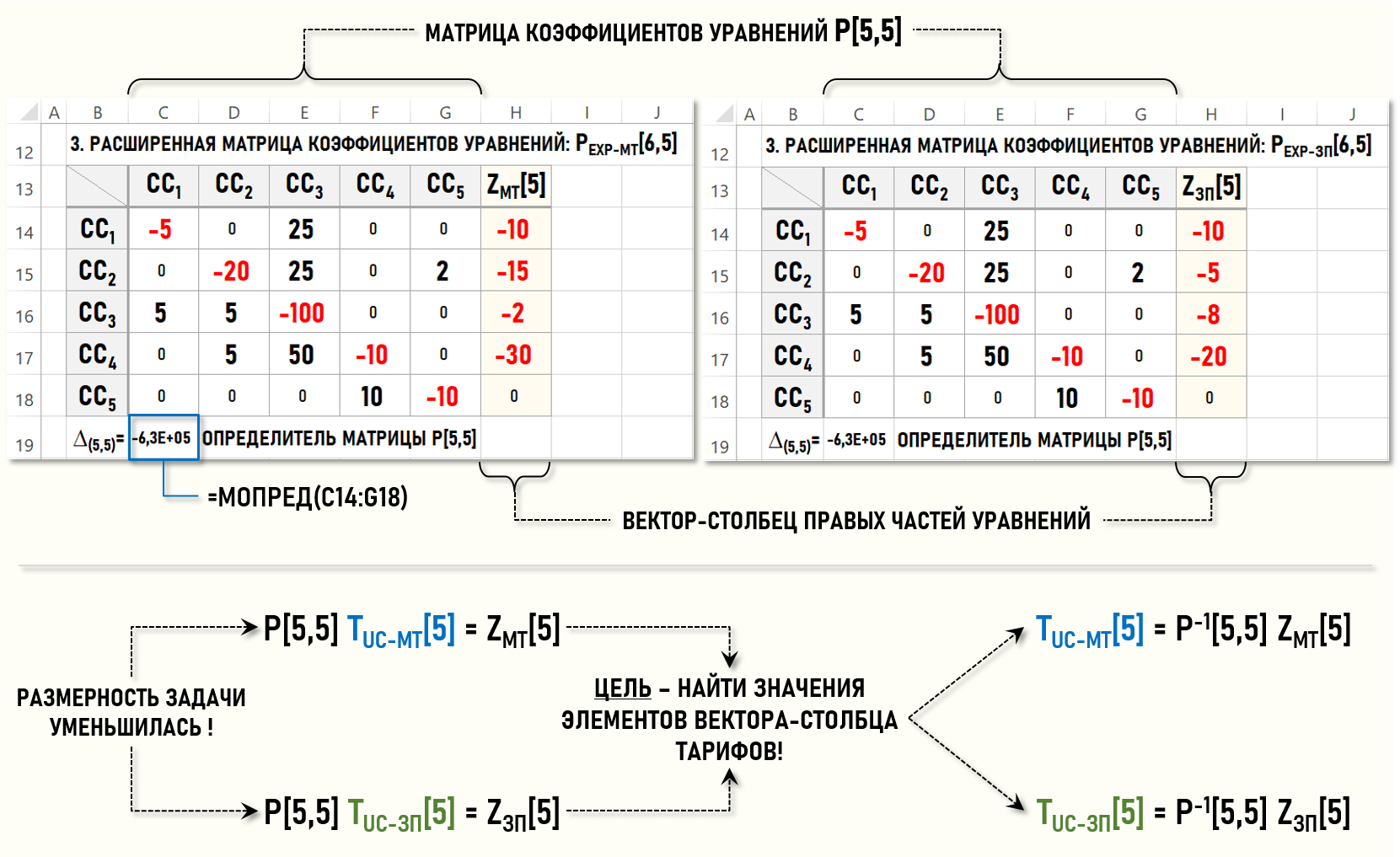
Это позволяет уменьшить число уравнений в обеих СЛАУ с 7-ми до 5-ти. Исключив из рассмотрения столбцы и строки для стоков CC₆ и CC₇, получим расширенные матрицы коэффициентов уравнений уменьшенной размерности:

   

 

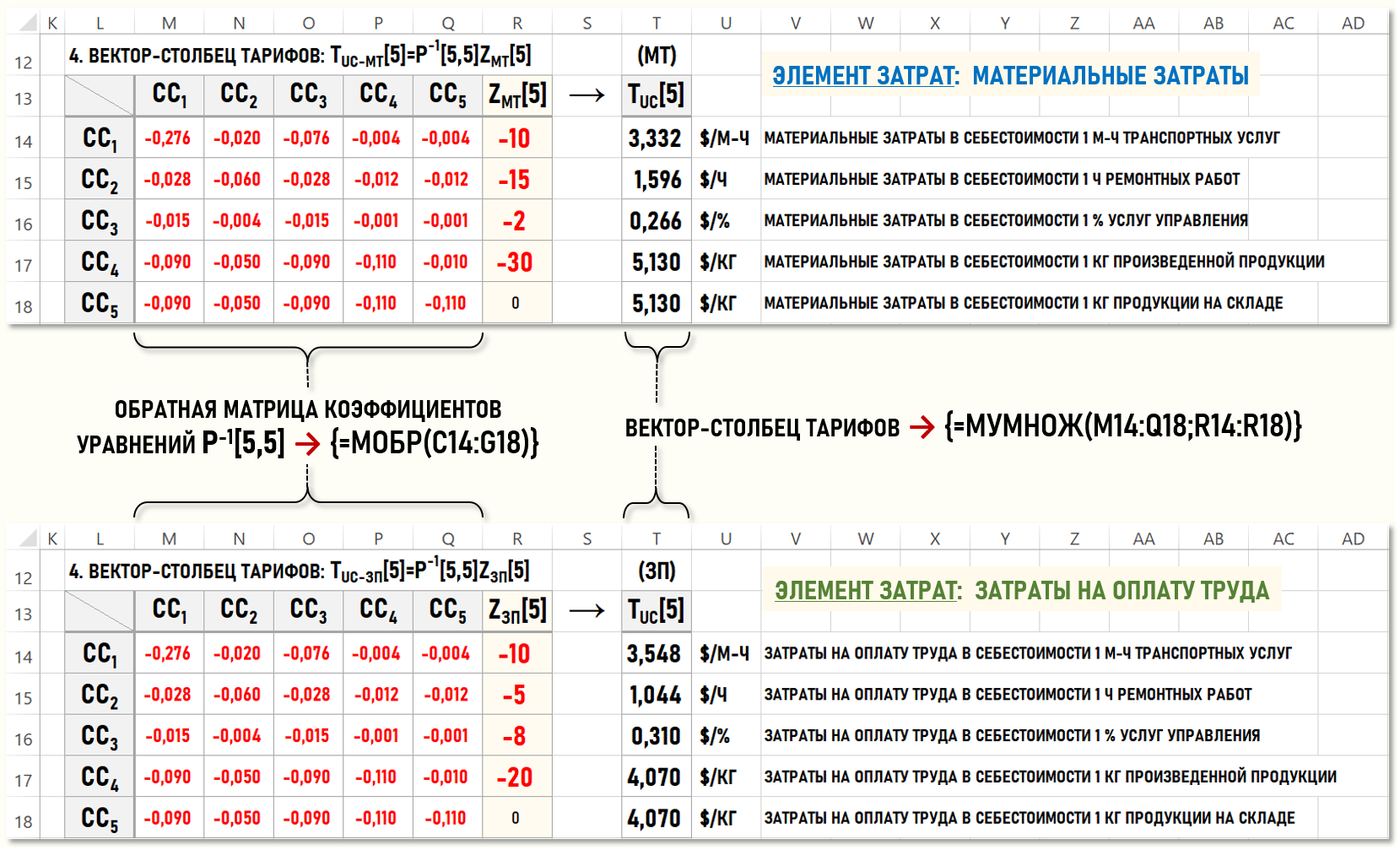
Вычисленное в ячейке С19 значение определителя матрицы коэффициентов уравнений Р[5,5] отлично от 0-ля, что позволяет найти решения СЛАУ. Для этого необходимо найти обратную матрицу коэффициентов уравнений Р^-1[5,5] и затем попарно перемножить ее с векторами Z_МТ[5] и Z_ЗП[5].

   

 

В результате будет сформирован вектор-столбец тарифов T_UC-МТ[5] для материальных затрат и вектор-столбец тарифов T_UC-ЗП[5] для затрат на оплату труда, т.е. будут найдены решения обеих СЛАУ.

  

МАТРИЦЫ СТОИМОСТЕЙ ДЛЯ ЭЛЕМЕНТОВ ЗАТРАТ  (↑)

  

Теперь осталось определить значения элементов матриц стоимостей C_МТ[7,7] и C_ЗП[7,7] для каждого элемента затрат, для чего надо умножить значения элементов матрицы исходных коэффициентов К[7,7] на соответствующие значения тарифов:

    

    

В ячейках матриц стоимостей C_МТ[7,7] и C_ЗП[7,7] содержатся искомые стоимости хозяйственных операций, которые теперь можно записать в ЖХО и показать в виде весов дуг в «нарисованном» Графе затрат.

Поскольку использование двух элементов затрат предполагает разделение Графа затрат на две компоненты связности, то если сгруппировать записи в ЖХО по элементам затрат – фактически мы получим два отдельных ЖХО для каждого элемента затрат. Покажем для наглядности записи в ЖХО отдельно для каждого элемента затрат.

Фрагмент ЖХО для стоимостей материальных затрат:

 

 

   

 

Фрагмент ЖХО для стоимостей затрат на оплату труда:

   

 

   

 

Также можно нарисовать Граф затрат, в котором потоки элементов затрат показаны с помощью кратных дуг. Такое представление позволяет наглядно увидеть «параллельные» движения потоков элементов затрат в модели для расчета себестоимости.

   

 

На рисунке с помощью диаграмм также показаны структуры стоимости первичных затрат подразделений предприятия в разрезе элементов затрат и структуры расходов предприятия в разрезе элементов затрат – себестоимостей проданных продукции и ремонтных работ.