Анализ безубыточности (5). Результаты расчета

    

Автор:  Александр Поляков

    

    

Процесс изучения материала данной части статьи предполагает, что параллельно с чтением статьи читатель будет работать с моделью для анализа безубыточности в Microsoft Excel (скачать таблицы).

Воспользуемся моделью и произведем поиск финансовых результатов от продажи дизтоплива и электроэнергии в следующем диапазоне значений исходного коэффициента k_5,6:

k_5,6=[50;650]  с шагом: ∆k_5,6=75 л – продажа дизтоплива

Выбранный диапазон изменения значений исходного коэффициента k_5,6 довольно велик, но его выбор объясняется тем, что мы не знаем заранее характер поведения Графа затрат во время проведения анализа безубыточности.

Количество продаваемой электроэнергии будем считать неизменным и зафиксируем его значение на уровне:

k_1,7=100 кВт∙ч     – количество проданной электроэнергии

Значение исходного коэффициента k_1,7 было выбрано исходя из предположения о том, что оно соответствует минимальной потребности покупателей в электроэнергии. При самостоятельной работе с моделью читатель может выбрать любое другое значение данного коэффициента.

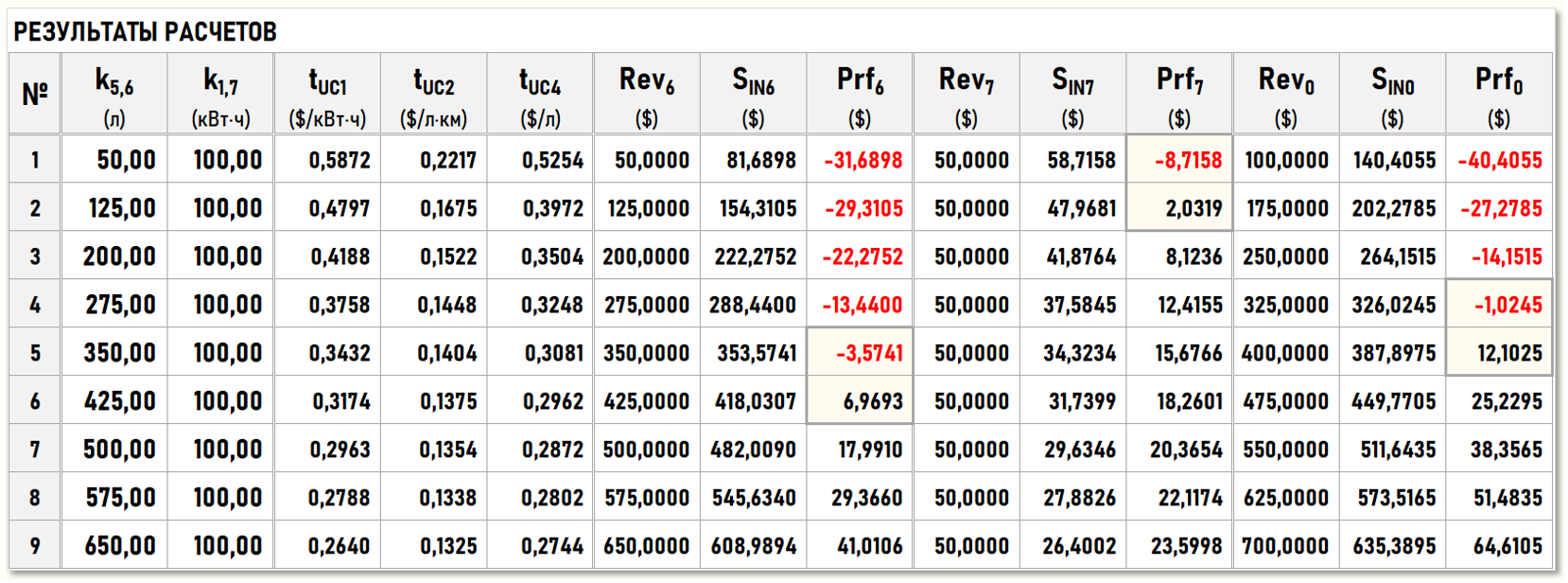
Произведем расчеты и представим полученные результаты в таблице:

   

    

Назначение столбцов таблицы были рассмотрены в предыдущей части статьи при обсуждении БЛОКА 1 модели. Представим также полученные значения с помощью диаграмм, отображающих поведение финансовых результатов (Prf_i):

   

   

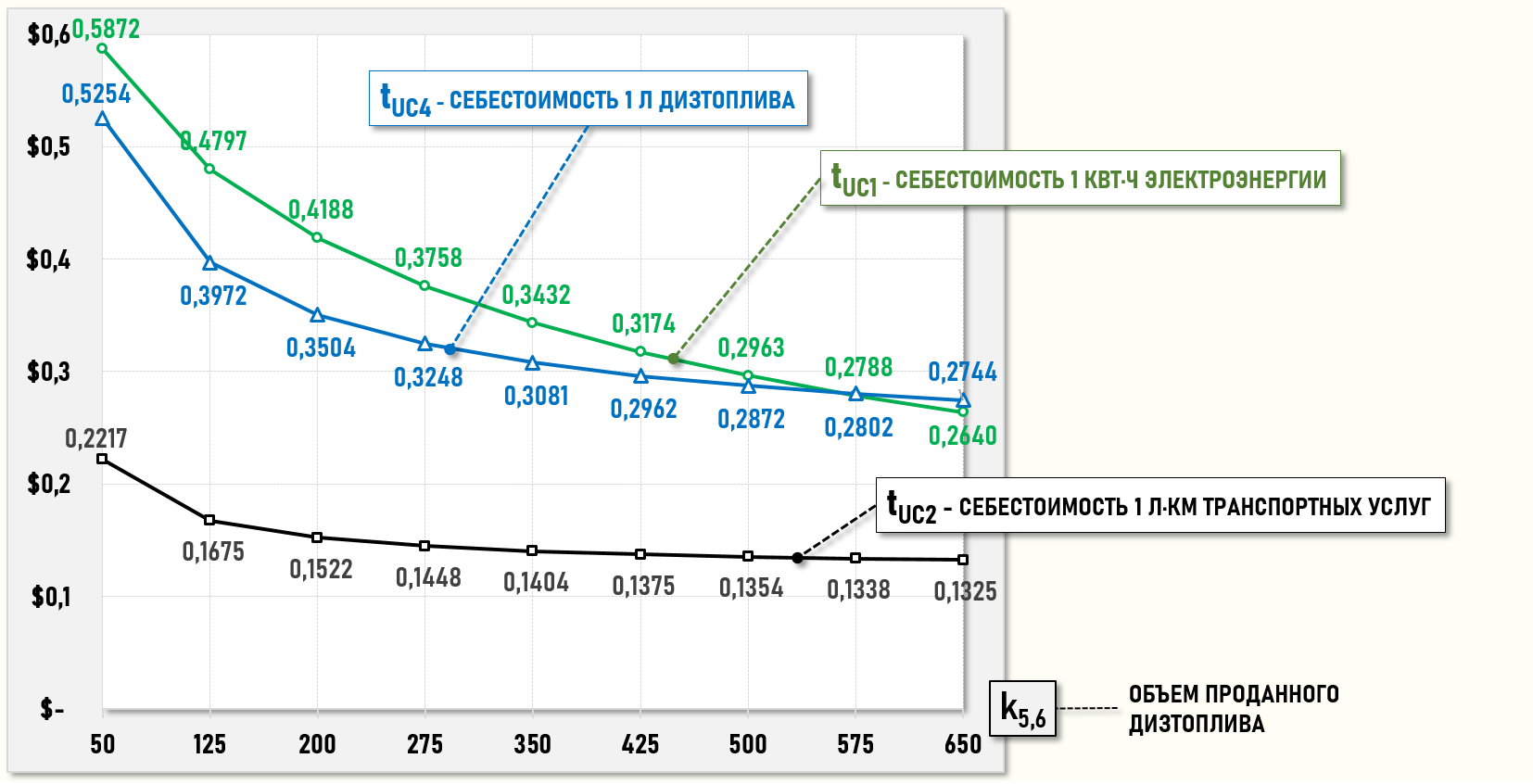
а также тарифов tUC1, t_UC2 и t_UC4:

 

На диаграммах видно, что характер изменения тарифов в процессе анализа безубыточности явно является нелинейным, поэтому применение разного рода «традиционных» общих линейных формул для анализа безубыточности отдельных видов деятельности предприятия привело бы к серьезным искажениям результата.

Более того, если бы в подсистеме НСИ для определения значений нормативных показателей использовались не постоянные величины, а какие-либо функциональные зависимости, то поведение тарифов могло бы иметь гораздо более нелинейный или кусочно-нелинейный характер. Но, поскольку мы использовали модель предприятия в виде Графа затрат, проведение анализа безубыточности и в этом случае не представило бы значительных сложностей.

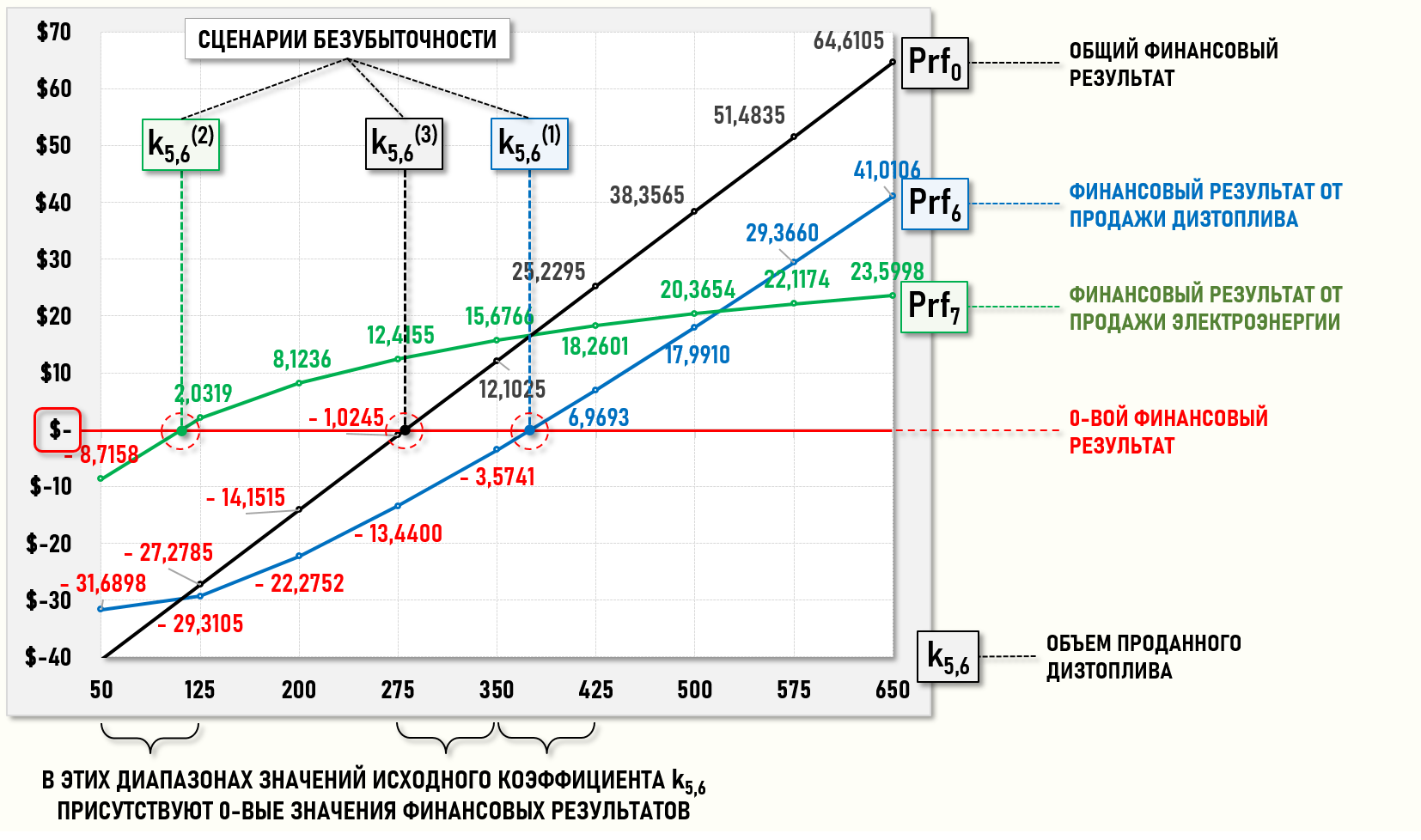
В таблице и на диаграммах видно, что в выбранном для анализа диапазоне значений исходного коэффициента k_5,6 существуют три сценария безубыточности – на диаграммах их можно увидеть в местах пересечения Prf_i с 0-вой отметкой оси ординат.

Можно выделить три диапазона значений исходного коэффициента k_5,6, на границах которых значения финансовых результатов Prf_i имеют противоположные знаки. Это означает, что внутри выделенных диапазонов обязательно найдется значение исходного коэффициента k_5,6, обеспечивающее 0-вой финансовый результат.

Выделим такие диапазоны значений k_5,6:

k_5,6=[350;425] – на границах диапазона значения Prf₆=[-3,5741; 6,9693]

k_5,6=[50;125] – на границах диапазона значения: Prf₇=[-8,7158; 2,0319]

k_5,6=[275;350] – на границах диапазона значения Prf₀=[-1,0245; 12,1025]

 

В каждом из этих диапазонов значений исходного коэффициента k_5,6 необходимо найти свой сценарий безубыточности (k_1,7=100 кВт∙ч – не изменяется):

k_5,6⁽¹⁾ – определяет количество проданного дизтоплива, при котором достигается 0-вой финансовый результат от его продажи: Prf₆(k_5,6⁽¹⁾)=0

k_5,6⁽²⁾ – определяет количество проданного дизтоплива, при котором достигается 0-вой финансовый результат от продажи электроэнергии в количестве 100 кВт∙ч: Prf₇(k_5,6⁽²⁾)=0

k_5,6⁽³⁾ – определяет количество проданного дизтоплива, при котором достигается общий 0-вой финансовый результат деятельности предприятия: Prf₀(k_5,6⁽³⁾)=0

 

Для поиска сценариев безубыточности далее можно использовать любой численный метод поиска корней уравнения Prf_i(k_5,6)=0. В нашем примере мы рассмотрим два способа, доступных каждому читателю, работающему в Microsoft Excel:

с помощью надстройки «Поиск решения» Microsoft Excel

с помощью инструмента «Подбор параметра» Microsoft Excel

   

ИСПОЛЬЗУЕМ НАДСТРОЙКУ «ПОИСК РЕШЕНИЯ» Microsoft Excel

 

Данная надстройка применяется для решения оптимизационных задач, предполагающих поиск значений аргументов, доставляющих целевой функции минимальное или максимальное значение при наличии каких-либо дополнительных ограничений.

Для поиска любого из трех сценариев безубыточности пользователю достаточно работать только с ячейками БЛОКА 1. Результаты вычислений.

 

    

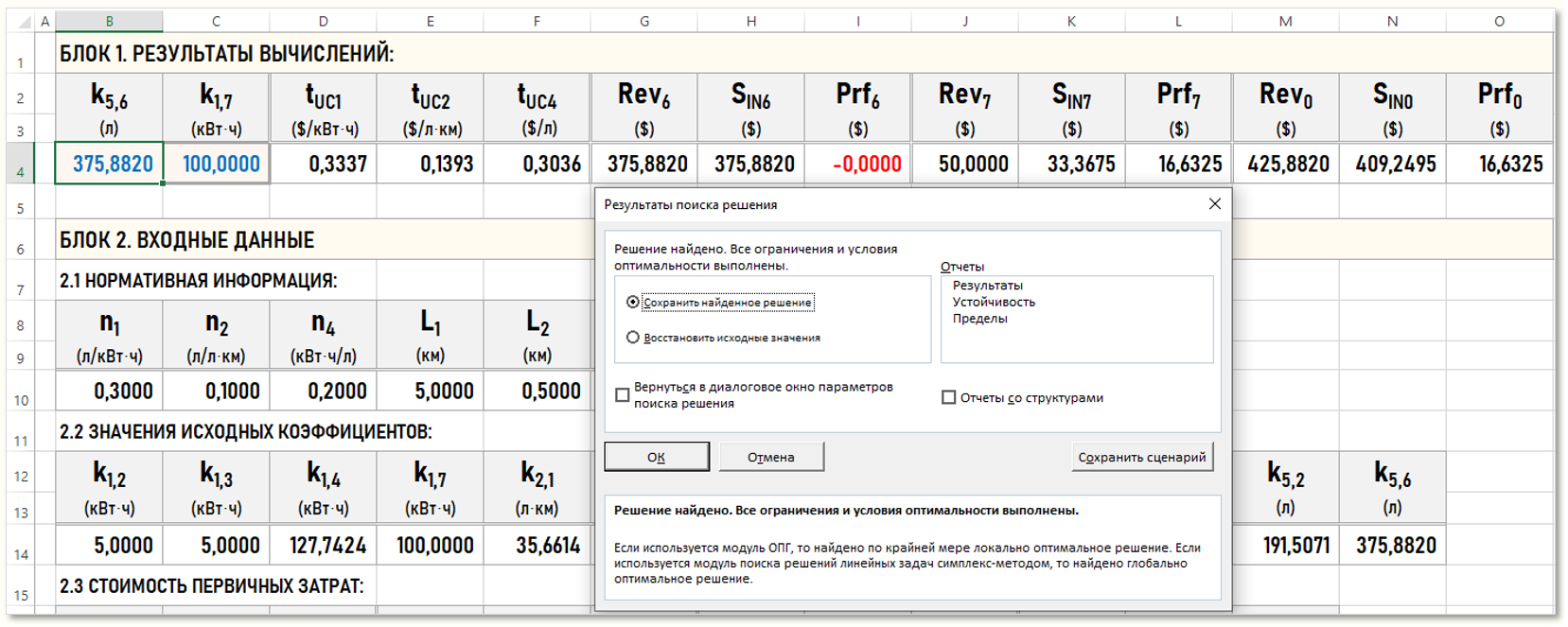
В качестве целевой функции выберем Prf₆ в ячейке I4 и будем оптимизировать ее значение до 0-ля, изменяя значение исходного коэффициента k_5,6 (ячейка B4) в диапазоне от 350 до 425. Нажав кнопку «Найти решение», получим результат:

 

  

Далее проделаем аналогичные действия для целевой функции Prf₇ в ячейке L4, изменяя значение исходного коэффициента k_5,6 (ячейка B4) в диапазоне от 50 до 125 и для целевой функции Prf₀ в ячейке O4, изменяя значение исходного коэффициента k_5,6 (ячейка B4) в диапазоне от 275 до 350. Полученные результаты представим в таблице:

    

 

ИСПОЛЬЗУЕМ ИНСТРУМЕНТ «ПОДБОР ПАРАМЕТРА» Microsoft Excel

 

Инструмент «Подбор параметра» Microsoft Excel является частью набора команд, которые называют средствами анализа «что-если». Этот инструмент работает почти так же, как «Поиск решения», только не позволяет вводить ограничения на значения изменяемых ячеек.

Сценарий поиска сценария безубыточности довольно прост:

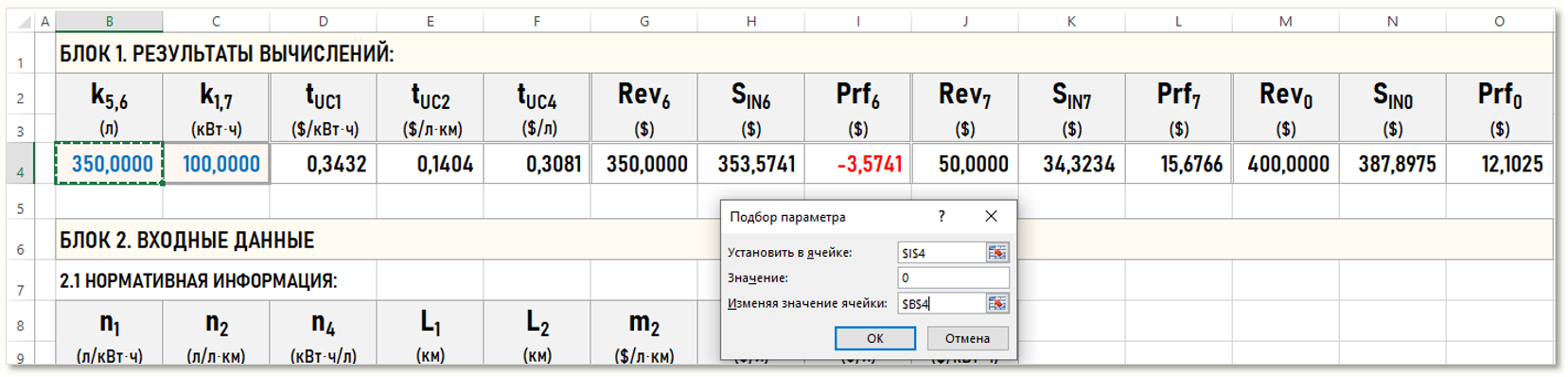
установим 0-вое значение Prf₆ в ячейке I4

изменяя значение исходного коэффициента k_5,6 в ячейке B4

 

 

Следует учесть, что данный инструмент более «капризен» к начальным данным параметров модели, чем надстройка «Поиск решения», поэтому в ячейку B4 мы ввели значение k_5,6=350 (л), соответствующее левой границе диапазона, в котором ищется сценарий безубыточности, иначе можно получить некорректный результат. 

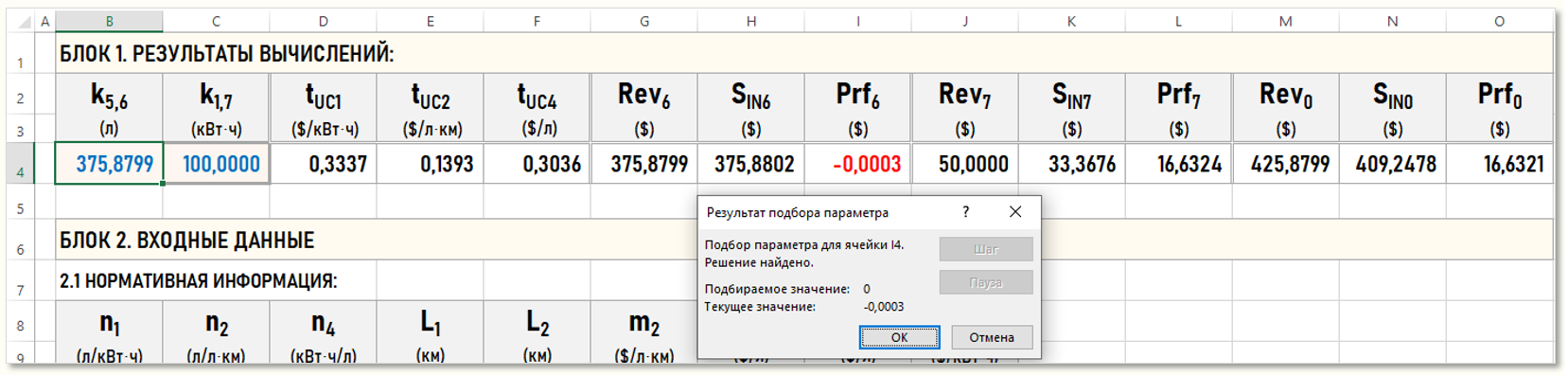
Нажмем ОК и получим результат для первого сценария безубыточности:

  

 

Как видим, финансовый результат Prf₆ в четвертом знаке после запятой отличен от о-ля, т.е. найденный результат менее точен, чем в предыдущем случае. Для решения нашей задачи это вполне приемлемая точность, но практика работы с моделями показывает, что предпочтительнее все-таки пользоваться надстройкой «Поиск решения», т.к. корректность работы «Подбора параметра» часто зависит от текущего значения в изменяемой ячейке.

Далее читатель может самостоятельно поработать с моделью, например, зафиксировав количество проданного дизтоплива и изменяя количество проданной электроэнергии, изменяя сразу оба количества, используя какие-либо правила определения норм для различных производственных программ и т.д. ... и т.п. Когда модель предприятия создана, пользователь может смело приступать к ее всестороннему исследованию и использованию для решения задач.

 

назад ...   далее ...