Прямые и обратные задачи на Графах затрат

Автор:  Александр Поляков

Напомним, что для расчета стоимости потоков затрат в Графе затрат G(N_G) используется математическая модель вида:

P[N_G,N_G]T_UC[N_G]=Z[N_G]

где:

P[N_G,N_G] – матрица коэффициентов уравнений

T_UC[N_G]   – вектор-столбец тарифов

Z[N_G]       – вектор-столбец правых частей уравнений

Принимая в качестве искомой каждую из трех входящих в формулу матриц, можно выделить три основных класса задач, которые могут быть решены на Графе затрат G(N_G).

Прямая задача (задача анализа) – сводится к нахождению значений элементов вектора-столбца тарифов T_UC[N_G] по заданным значениям элементов матрицы коэффициентов уравнений P[N_G,N_G] и вектора-столбца правых частей уравнений Z[N_G]. Другими словами, решение прямой задачи позволяет найти величины тарифов на выходах центров затрат когда для Графа затрат известны значения всех исходных коэффициентов, стоимости первичных затрат и затрат в незавершенном производстве на начало и конец рассматриваемого периода. По-существу, это «обычная» задача расчета себестоимости произведенной и проданной продукции (работ, услуг).

Обратная задача (задача синтеза) – сводится к определению значений элементов вектора-столбца правых частей уравнений Z[N_G] в предположении, что известны значения элементов матрицы коэффициентов уравнений P[N_G,N_G] и вектора-столбца тарифов T_UC[N_G]. Подобные задачи обычно решаются в процессе финансового планирования, когда задаются целевые значения себестоимости производства и продажи продукции (работ, услуг) и требуется определить стоимости первичных затрат, необходимые для получения искомой себестоимости. При этом структура модели предприятия – Графа затрат, заданная матрицей коэффициентов уравнений P[N_G,N_G], также считается известной.

Задача настройки модели – самая сложная из перечисленных задач. В результате решения данной задачи формируется матрица коэффициентов уравнений P[N_G,N_G] Графа затрат G(N_G). Задачи данного класса также можно отнести к классу обратных задач, в процессе решения которых необходимо определить структуру модели предприятия.

Под обратной задачей, в общем случае, будем понимать задачу определения количественных характеристик явления по результатам измерений их косвенных проявлений. Сложность подобных задач состоит в том, что разные причины могут приводить к очень близким косвенным проявлениям. Иначе говоря, обратная задача является, как правило,  некорректной.

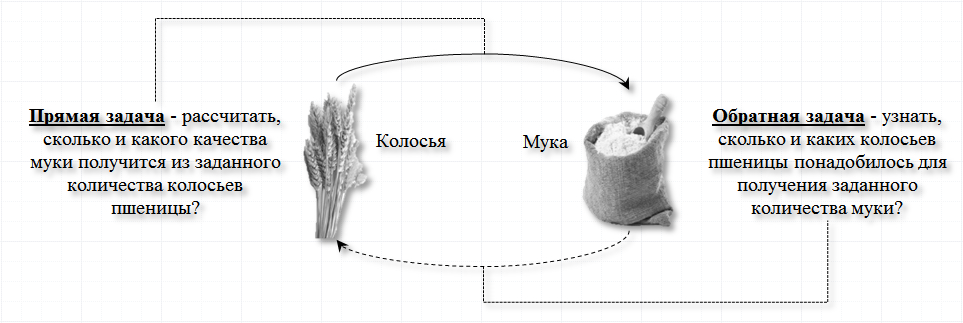
Рассмотрим пример. Предприятие производит пшеничную муку из зерен пшеницы, которые, в свою очередь, содержатся в колосьях пшеницы. Зная особенности производственного процесса и характеристики исходных колосьев можно получить вполне достоверную информацию о том, сколько и какого качества муки получится на выходе. Это прямая задача.

Если же мы, имея в своем распоряжении некоторое количество муки определенного качества, захотим узнать – сколько и каких колосьев пшеницы понадобилось для ее производства, то для этого придется решать обратную задачу.

В современном естествознании существует обширный класс задач, которые можно отнести к классу некорректно поставленных задач. В перечень таких задач попадают, например,  задачи обработки наблюдений без дополнительной количественной информации о свойствах решений. В общем случае, классы корректно поставленных задач и некорректно поставленных задач различаются степенью определенности их решений.

Задача называется корректной, т.е. корректно поставленной, если выполняются условия, сформулированные французским математиком Ж.Адамаром[1], и называемые условиями корректности:

• условие существования решения задачи

• ­условие однозначности решения задачи

• ­условие устойчивости решения задачи

Смысл условия существования решения задачи заключается в том, что среди исходных данных отсутствуют противоречащие друг другу условия, что исключало бы возможность решения задачи, т.е. задача имеет решение при любых допустимых исходных данных.

Условие однозначности решения задачи означает, что исходных данных достаточно для однозначной определенности решения задачи.

Оба вышеперечисленных условия обычно называют условиями математической определенности задачи.

Условие устойчивости решения задачи обычно трактуется как физическая детерминированность задачи. Это объясняется тем, что исходные данные задачи, как правило, задаются с некоторой погрешностью. При нарушении условия устойчивости решения задачи как угодно малые возмущения исходных данных могут вызывать как угодно большие отклонения в решении.

Задачи, не удовлетворяющие хотя бы одному из трех вышерассмотренных условий корректности, называются некорректными задачами или некорректно поставленными задачами.

В литературном языке слово «корректный» означает – вежливый, тактичный, учтивый. В математических текстах этот термин применяется в несколько ином смысле[2], заменяя такие термины, как «правильный», «верный». С появлением в 1932 году статьи французского математика Жака Адамара, словосочетание корректная задача стало означать в математической физике задачу с вежливым, тактичным поведением. Соответственно невыполнение условий корректности для решаемой задачи позволяет оценить ее поведение как невежливое. Такие задачи раньше казались математическими чудовищами и их всемерно старались избегать.

Как говорилось выше, решение прямых задач связано с отысканием следствия некоторого процесса по известной причине. Например, можно на любой момент времени рассчитать положения планет Солнечной системы, зная главную причину, лежащую в основе их движения – закон всемирного тяготения Ньютона с поправками на эффекты общей теории относительности.

В отличие от прямых задач, трудности решения обратных задач связаны с тем, что один и тот же эффект может быть порожден разными причинами. Например, если нагреть воду при нормальном атмосферном давлении до температуры 100°C, то она закипит. Но, из того факта, что вода кипит, вовсе не следует, что она нагрета до температуры 100°C, т.к. вода может кипеть и при комнатной температуре, но при низком атмосферном давлении. В горах вода может кипеть при температуре около 80°C, т.е. эффект кипения воды может быть вызван разными причинами – либо высокой температурой, либо низким давлением.

Для решения прямой задачи достаточно иметь представление о причинно-следственной связи входных данных и выходных параметров (реакции) модели. Для решения обратной задачи необходимо учитывать уже целое множество причинно-следственных связей, имеющих отношение к изучаемому объекту, т.е. надо иметь значительно более богатый опыт и экспериментальный материал, чем для решения прямой задачи.

К середине 20-го века у математиков накопился ряд вопросов – что понимать под приближенным решением обратной задачи, как определить приближенное решение, чтобы оно оказалось устойчивым к малым изменениям входных данных, каков практический алгоритм построения приближенных решений в конкретных задачах?

Исчерпывающих ответов на эти вопросы не было, и вплоть до 60-х годов 20-го века многие математики и физики утверждали, что корректность задачи выражает ее физическую определенность и является принципиальным условием для возможности математического моделирования реальных ситуаций. На некорректные задачи смотрели как на некие досадные недоразумения, а на попытки их решения было наложено своеобразное математическое вето.

Некоторое время такой же точки зрения придерживался и выдающийся советский математик Андрей Николаевич Тихонов. В учебнике по уравнениям математической физики издания 1951 года Тихонов А.Н. и его ученик Самарский А.А. утверждали, что тратить время на решение некорректно поставленных задач нецелесообразно. Потребовалось еще немногим более 10-ти лет, чтобы, благодаря работам Тихонова А.Н., Лаврентьева М.М., Иванова В.К. и других математиков, мировая математическая наука отказалась от прежней точки зрения. Сейчас можно говорить о научной школе Тихонова А.Н., создавшей математическую теорию некорректно поставленных задач и разработавшей эффективные методы их решения – регуляризирующие алгоритмы.

Некорректно поставленные задачи можно рассматривать как физически недоопределенные, плохо поставленные, множества их приближенных решений очень широки, а иногда и вовсе не имеют границ. Это означает, что некорректные задачи нужно доопределить, т.е. предоставить дополнительную информацию об искомом решении, вытекающую из опыта всесторонних исследований рассматриваемого объекта. Эта дополнительная информация должна быть известна до момента решения некорректной задачи, она должна позволить сформулировать критерий отбора нужного приближенного решения из множества приближенных решений задачи и построить регуляризирующий алгоритм. Такой информацией могут служить, например, априорные сведения о гладкости искомого решения, его монотонности, выпуклости, неотрицательности и т. п.

Применительно к теме сайта, к классу некорректно поставленных задач можно отнести задачи, связанные с планированием себестоимости на Графах затрат. В данных задачах, как правило, считаются известными значения себестоимости произведенной и/или проданной продукции (работ, услуг) в рамках заданного набора видов деятельности предприятия. В результате решения задачи планирования необходимо определить индивидуальную топологию Графа затрат, позволяющую получить заданные значения себестоимости. Понятно, что одни и те же значения себестоимости продукции (работ, услуг) могут быть получены с помощью различных индивидуальных топологий Графов затрат. Следовательно, решение задачи планирования себестоимости на Графе затрат предполагает не только умение формировать матрицы, участвующие в матричной форме представления СЛАУ, но и получение дополнительной информации о хозяйственных процессах, протекающих как внутри Графа затрат, так и внутри отдельных центров затрат.