Решение обратной задачи на Графе затрат. Пример 1
Автор: Александр Поляков
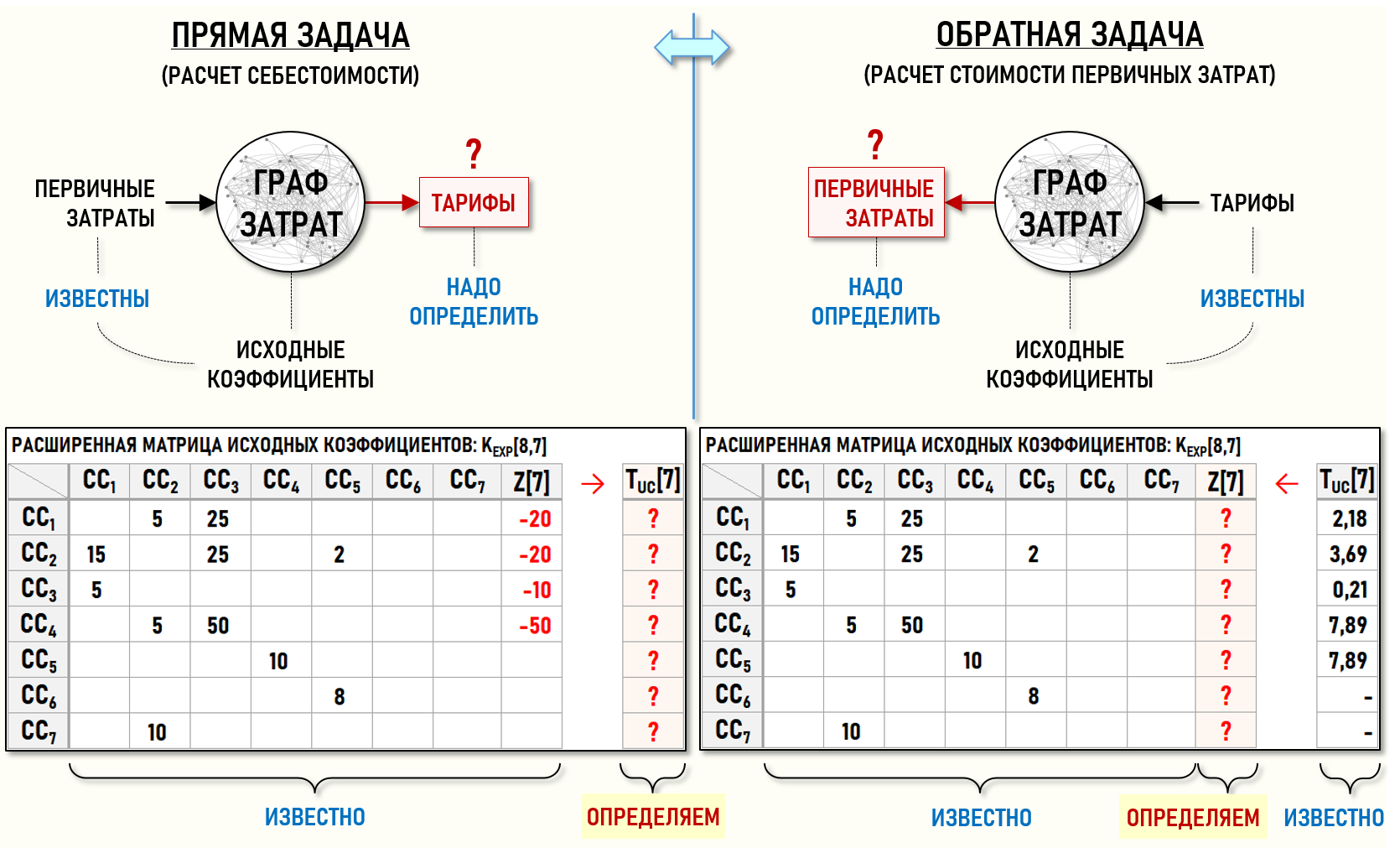
В данной статье мы рассмотрим простейший класс обратных задач, решаемых с помощью Графов затрат. Простейших в том смысле, что, имея детерминированную многофакторную математическую модель хозяйственной деятельности предприятия в виде СЛАУ, мы можем с ее помощью с одинаковым успехом решить на Графе затрат как прямую, так и обратную задачу. Напомним, что обратная задача в принципе является некорректной и может иметь несколько решений, но в статье мы рассмотрим самую простую ситуацию, когда можно получить единственное решение обратной задачи.
Под прямой задачей в данном случае будем понимать задачу расчета себестоимости продукции, работ и услуг, т.е. задачу поиска значений тарифов на выходе всех центров затрат Графа затрат для случая, когда заранее известны стоимости первичных затрат и значения исходных коэффициентов. Другими совами, это обычная задача расчета себестоимости, которая регулярно решается на каждом предприятии.
Под обратной задачей будем понимать задачу определения стоимости первичных затрат при заранее заданных значениях тарифов и исходных коэффициентов. Другими словами, мы сами задаем желаемые значения тарифов, т.е. фактически задаем желаемые значения себестоимости продукции, работ и услуг, и далее определяем, при каких стоимостях первичных затрат они могут быть получены. Такие задачи также можно отнести к «обычным» задачам, в том или ином виде они решаются на любом предприятии, например, при финансовом планировании его хозяйственной деятельности.
Рассмотрим эти два класса задач на примере небольшого предприятия, которое в отчетном периоде производит и продает продукцию и выполняет (продает) для сторонних контрагентов небольшие объемы ремонтных работ.
Цех 1 (СС1) в отчетном периоде оказал транспортные услуги Цеху 2 (15м-ч) и Офису предприятия (5м-ч). Объемы транспортных услуг измеряются в машино-часах.
Цех 2 (СС2) в отчетном периоде выполнил ремонтные работы для Цеха 1 (5ч), для Цеха 4 (5ч) и для сторонних контрагентов (10ч), т.е. продал ремонтные работы. Объемы ремонтных работ измеряются в часах. Себестоимость проданных ремонтных работ формируется на входе центра затрат СС7.
Цех 4 (СС4) произвел в отчетном периоде 10кг продукции и поместил ее на склад предприятия (СС5). Часть продукции со склада (2кг) в отчетном периоде была использована Цехом 2, а оставшаяся продукция (8кг) была продана покупателям. Себестоимость проданной продукции формируется на входе центра затрат СС6.
Управление деятельностью предприятия производится административным персоналом в Офисе (СС3). В данном примере рассчитываются полные себестоимости проданных продукции и ремонтных работ. Распределение стоимости управленческих затрат Офиса (СС3) производится в следующих пропорциях – по 25% получают Цех 1 и Цех 2, а оставшиеся 50% приходятся на долю Цеха 4.
РЕШАЕМ ПРЯМУЮ ЗАДАЧУ
Ниже на рисунке представлен журнал хозяйственных операций (ЖХО) и взвешенный Граф затрат G(7,11) предприятия в отчетном периоде – до решения прямой задачи, т.е. до выполнения процедуры закрытия затрат периода:
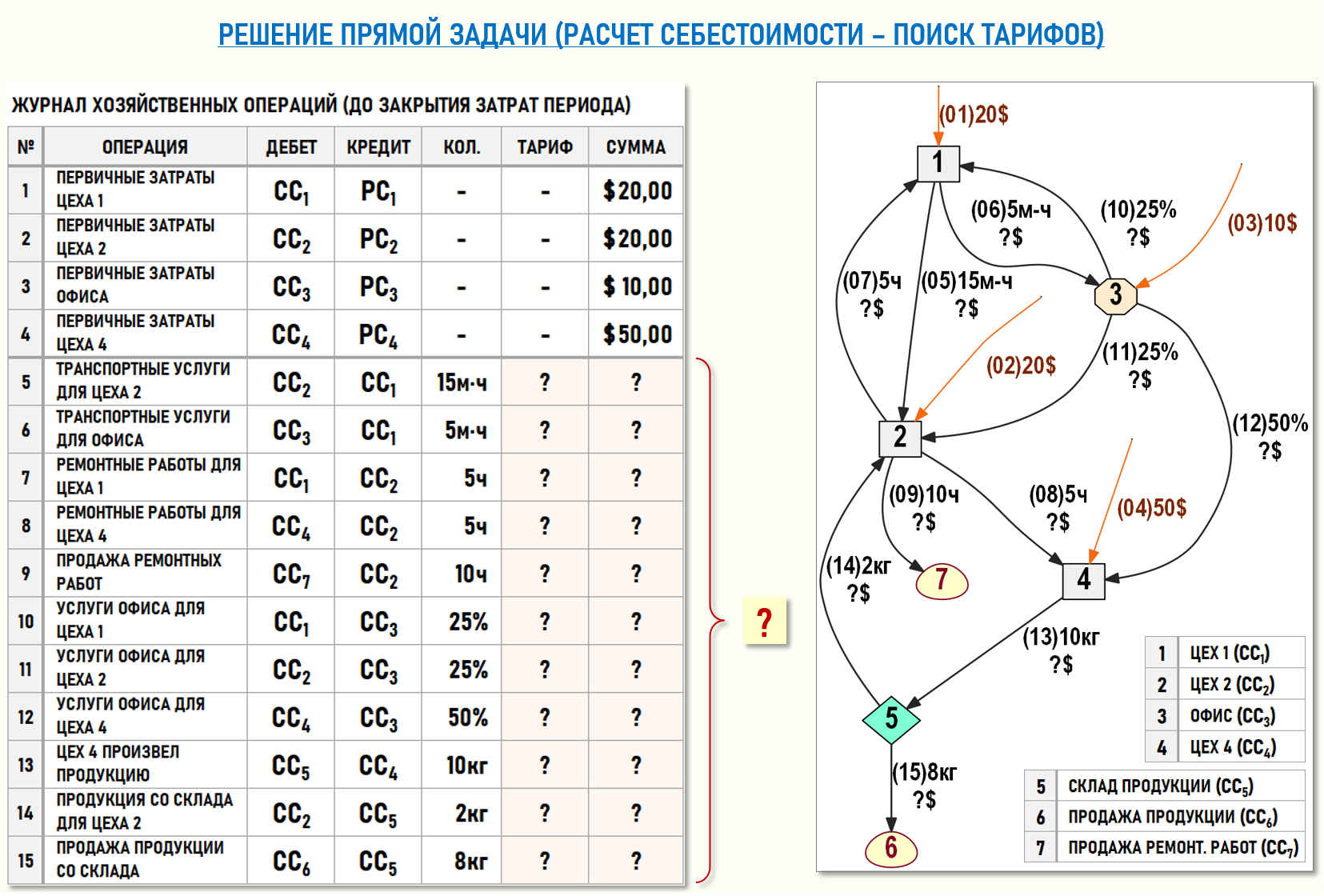
Алгоритм решения такой прямой задачи, связанной с расчетом себестоимости, нам уже хорошо известен из предыдущих статей. Можно скачать связанные таблицы Microsoft Excel для расчета себестоимости (решения СЛАУ) и проверить решение, а мы сразу посмотрим полученные результаты. Ниже на рисунке представлен ЖХО и взвешенный Граф затрат G(7,11) после решения прямой задачи.
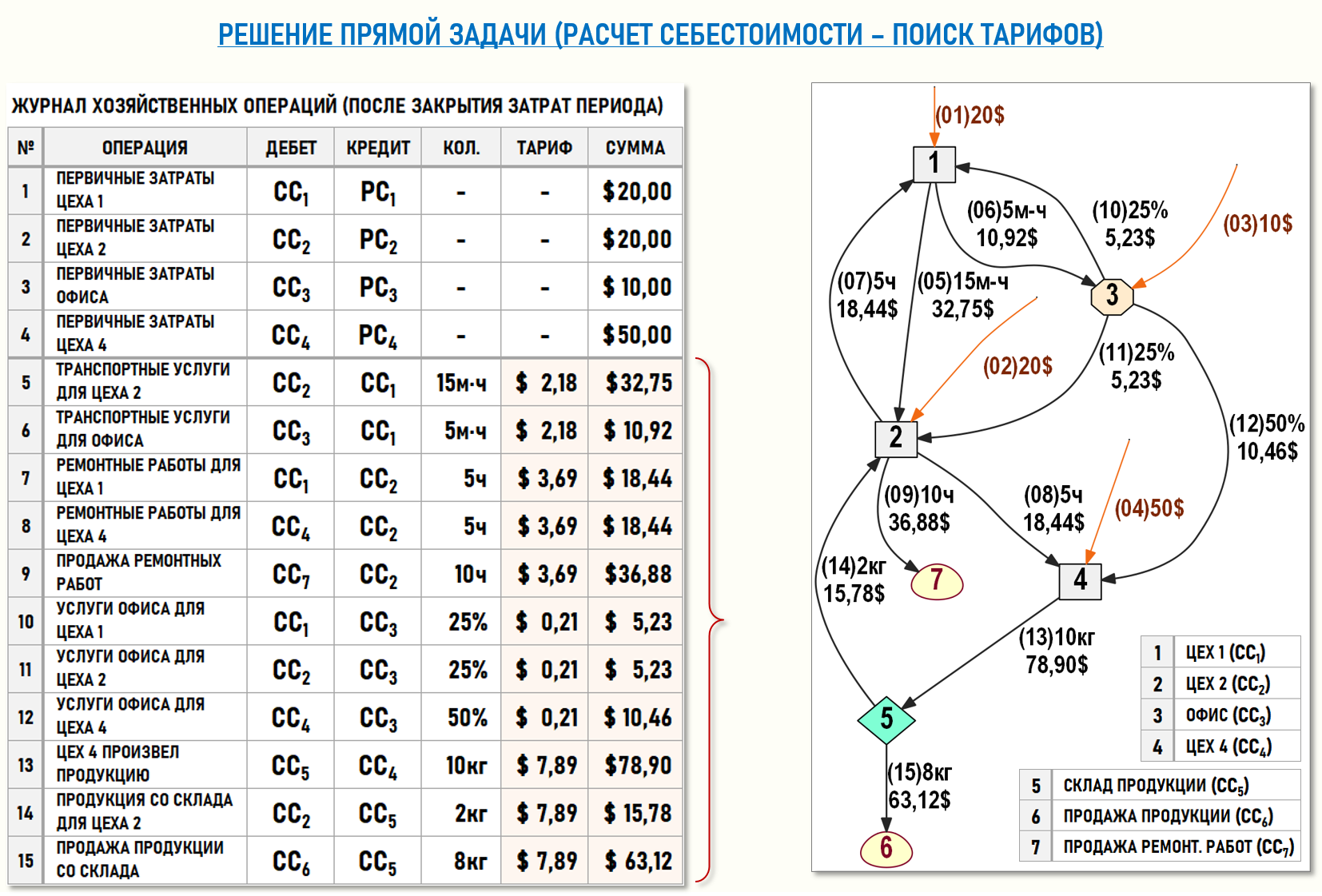
Прямая задача решена, теперь решим обратную задачу – по известным значениям тарифов и исходных коэффициентов определим стоимости первичных затрат.
РЕШАЕМ ОБРАТНУЮ ЗАДАЧУ
Граф затрат G(7,11) для решения обратной задачи в качестве весов дуг содержит количества и стоимости вторичных затрат, а стоимости первичных затрат необходимо определить. Поскольку стоимости вторичных затрат определяются как произведения тарифов и исходных коэффициентов, то до начала решения обратной задачи значения тарифов предполагаются известными.
ЖХО и взвешенный Граф затрат G(7,11) до решения обратной задачи, т.е. до поиска стоимостей первичных затрат, имеет следующий вид:
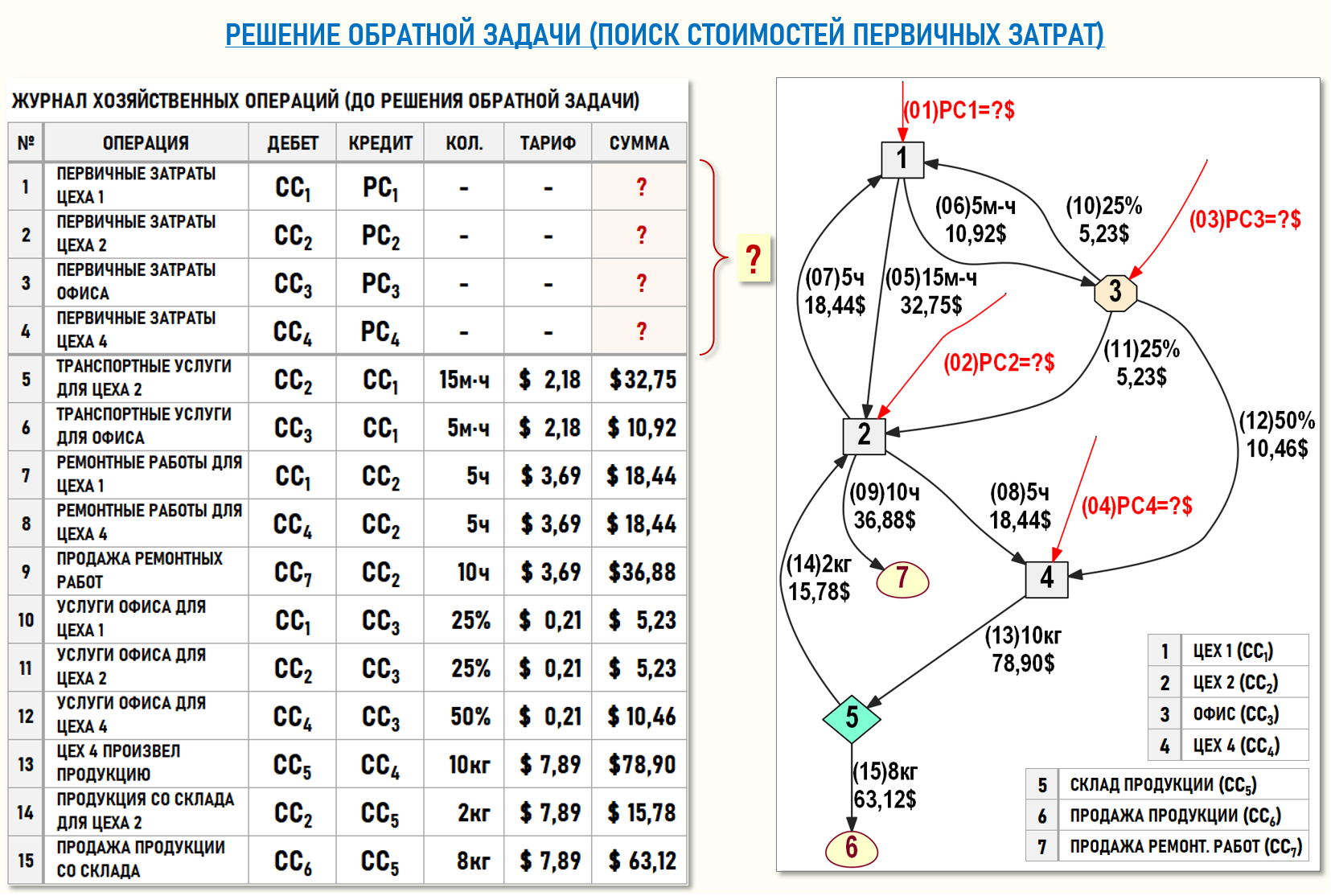
Для решения обратной задачи вспомним, как выглядит матричная форма записи СЛАУ для Графа затрат G(7,11) из нашего примера:
Z[7]=P[7,7] TUC[7]
где:
P[7,7] – матрица коэффициентов уравнений, она легко получается из матрицы исходных коэффициентов K[7,7], которая нам известна
TUC[7] – вектор-столбец тарифов, который также считается известным
Z[7] – вектор-столбец правых частей уравнений, значения элементов которого предстоит определить в процессе решения обратной задачи
Данная задача относится к классу детерминированных обратных задач, мы можем найти ее единственное решение. Стоимость любого потока вторичных затрат ci,j определяется как произведение исходного коэффициента ki,j на тариф tUCi:
ci,j=ki,j×tUCi
поэтому задачу можно сформулировать также следующим образом – по заданным значениям стоимостей потоков вторичных затрат ci,j необходимо определить стоимости первичных затрат pci на входах центров затрат Графа затрат G(7,11).
Напомним, что в расчете значений элементов вектор-столбца правых частей уравнений zi принимают участие не только стоимости первичных затрат pci, но и стоимости затрат в незавершенном производстве на начало и на конец периода:
zi=wpENDi−wpBEGi−pci
Это значит, что в общем случае нашу обратную задачу необходимо доопределить, т.е. получить дополнительную информацию о том, как соотносятся между собой стоимости первичных затрат и затрат в незавершенном производстве на начало и на конец периода. В нашем примере для простоты будем считать, что во всех центрах затрат стоимости затрат в незавершенном производстве на начало и на конец периода отсутствуют.
Перемножив матрицы P[7,7] и TUC[7], найдем значения элементов вектора-столбца правых частей уравнений Z[7] (скачать таблицы Microsoft Excel):
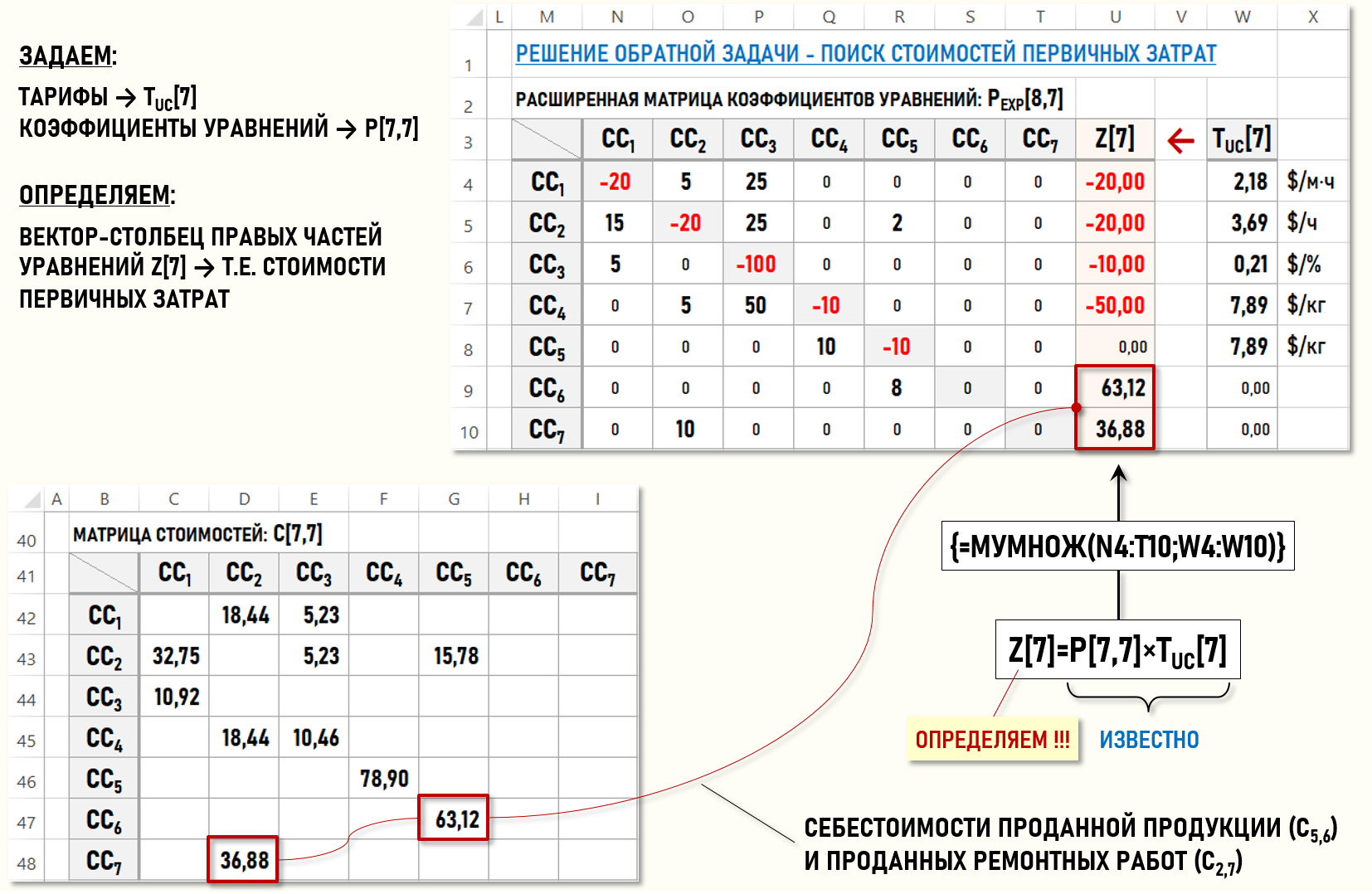
Как видно выше на рисунке, при перемножении матриц P[7,7] и TUC[7] были определены не только стоимости первичных затрат (со знаком «–») в ячейках (U4:U7), но и себестоимость проданной продукции (U9) и себестоимость проданных ремонтных работ (U10). Это объясняется тем, что центры затрат CC6 и CC7 являются стоками, и все пришедшие в них потоки затрат остаются в них в качестве затрат незавершенного производства на конец периода (в терминологии Графов затрат), формируя значения соответствующих элементов вектора-столбца Z[7].
Ниже на рисунке представлен ЖХО и взвешенный Граф затрат G(7,11) после решения обратной задачи:
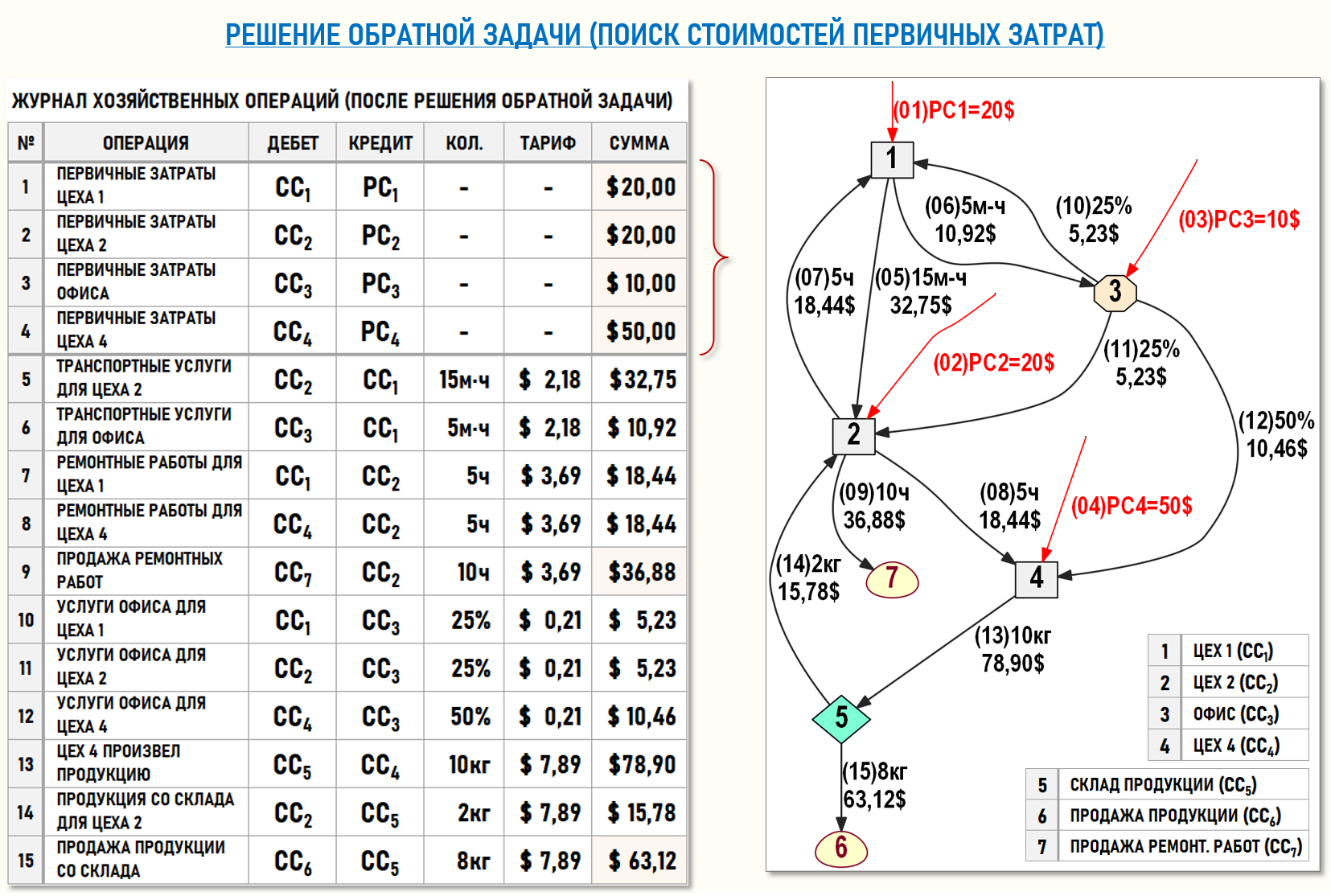
Обратная задача решена – стоимости первичных затрат найдены.

