Устойчивость решения обратной задачи (планирование)

 

Автор:  Александр Поляков

    

В данной статье рассмотрен пример расчета, проводимого в процессе выполнения процедуры финансового планирования себестоимости на Графе затрат. В примере изучается ситуация, при которой небольшое изменение планируемого (в пределах 1%) тарифа для транспортных услуг приводит к очень большим изменениям стоимостей первичных затрат (более, чем на ± 50%) в транспортном и ремонтном цехах предприятия.

   

РЕШЕНИЕ ПРЯМОЙ ЗАДАЧИ

    

Обсудим третье условие корректности обратной задачи – условие устойчивости решения задачи. Рассмотрим его смысл на примере решения прямой и обратной задачи на Графе затрат G₁(4,4), представляющем собой модель небольшого предприятия, состоящего всего из двух цехов:

 

 

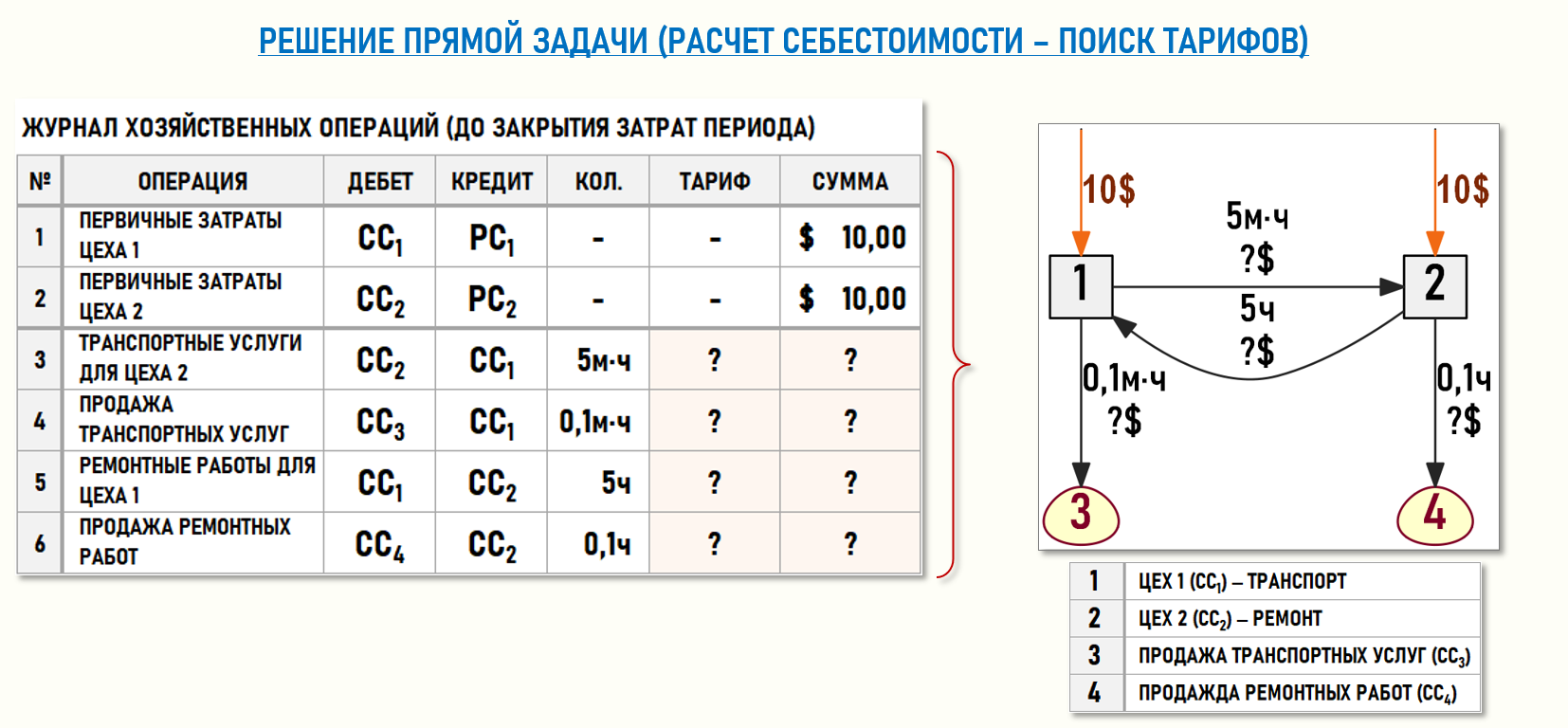
Цех 1 (CC₁) оказывает транспортные услуги Цеху 2 предприятия и продает эти услуги сторонним контрагентам. Объемы транспортных услуг измеряются в машино-часах. Себестоимость проданных транспортных услуг формируется на входе центра затрат CC₃.

Цех 2 (CC₂) выполняет ремонтные работы для Цеха 1 предприятия и для сторонних контрагентов, т.е. продает эти работы. Объемы ремонтных работ измеряются в часах. Себестоимость проданных ремонтных работ формируется на входе центра затрат CC₄.

Предприятие только начинает свою производственную деятельность, поэтому в первый отчетный период были проданы очень маленькие объемы транспортных услуг и ремонтных работ:

k_1,3=0,1 м-ч – проданы транспортные услуги

k_2,4=0,1 ч – проданы ремонтные работы

Остальное время сотрудники Цеха 2 (CC₂) занимались ремонтом автотранспорта, работающего в Цехе 1 (CC₁), а сотрудники Цеха 1 (CC₁) обеспечивали доставку запасных частей для производства ремонтных работ и доставку сотрудников Цеха 2 (CC₂) до места работы. В результате, объемы транспортных услуг и ремонтных работ для внутренних нужд предприятия в первом отчетном периоде составили:

k_1,2=5 м-ч – оказаны транспортные услуги для Цеха 2 (CC₂)

k_2,1=5 ч – выполнены ремонтные работы для Цеха 1 (CC₁)

В первом отчетном периоде цехами предприятием были получены следующие стоимости первичных затрат (зарплата, материалы и т.д.):

pc₁⁽¹⁾=10$

pc₂⁽¹⁾=10$

Решим СЛАУ и получим стоимости тарифов (скачать таблицы для решения СЛАУ):

t_UC1⁽¹⁾=100 $/м-ч – себестоимость 1-го машино-часа

t_UC2⁽¹⁾=100 $/ч – себестоимость 1-го часа ремонтных работ

что позволит сформировать матрицу стоимостей C⁽¹⁾[4,4] и взвешенный Граф затрат G₁(4,4) с весами дуг, характеризующими стоимости вторичных затрат: 

    

 

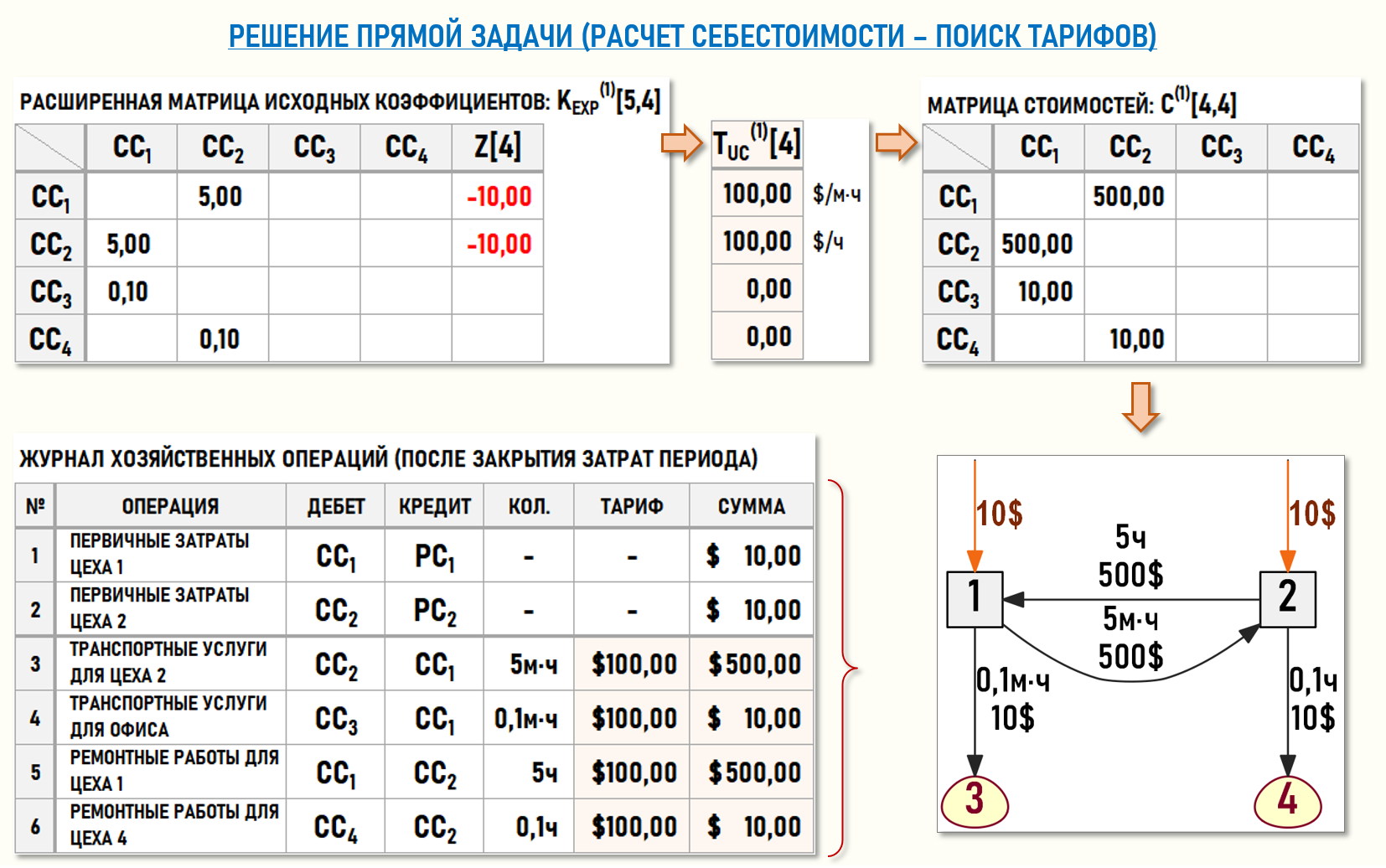
Наличие встречных потоков вторичных затрат между транспортным и ремонтным цехами привело к тому, что величины обоих тарифов многократно превышают как стоимости первичных затрат, поступивших в каждый из цехов в рассматриваемом периоде, так и общую сумму первичных затрат предприятия. Это не должно удивлять читателя, знакомого с теорией Графов затрат, т.к. такие большие величины тарифов являются прямым следствием применяемой в бухгалтерском учете балансовой модели для расчета себестоимости. Стоимости встречных вторичных затрат в этой модели являются сугубо расчетными величинами, подробнее об этом можно прочитать в статьях:

Как появляются встречные затраты

«Большие» стоимости встречных затрат

   

РЕШЕНИЕ ОБРАТНОЙ ЗАДАЧИ

      

Перейдем к решению обратной задачи на Графе затрат G₁(4,4) – определим стоимости первичных затрат, необходимых Цеху 1 (CC₁) и Цеху 2 (CC₂) для случая, когда себестоимость 1-го машино-часа транспортных услуг (t_UC1) уменьшится на 1%:

t_UC1⁽²⁾=t_UC1⁽¹⁾×0,99=100×0,99=99 $/м-ч

Себестоимость 1-го часа ремонтных работ (t_UC2) и объемы транспортных услуг и ремонтных работ остаются неизменными. Это значит, что матрица исходных коэффициентов K[4,4], как и матрица коэффициентов уравнений P[4,4], останется неизменной, а вектор-столбец тарифов T_UC⁽²⁾[4] примет следующий вид (скачать таблицы):

 

     

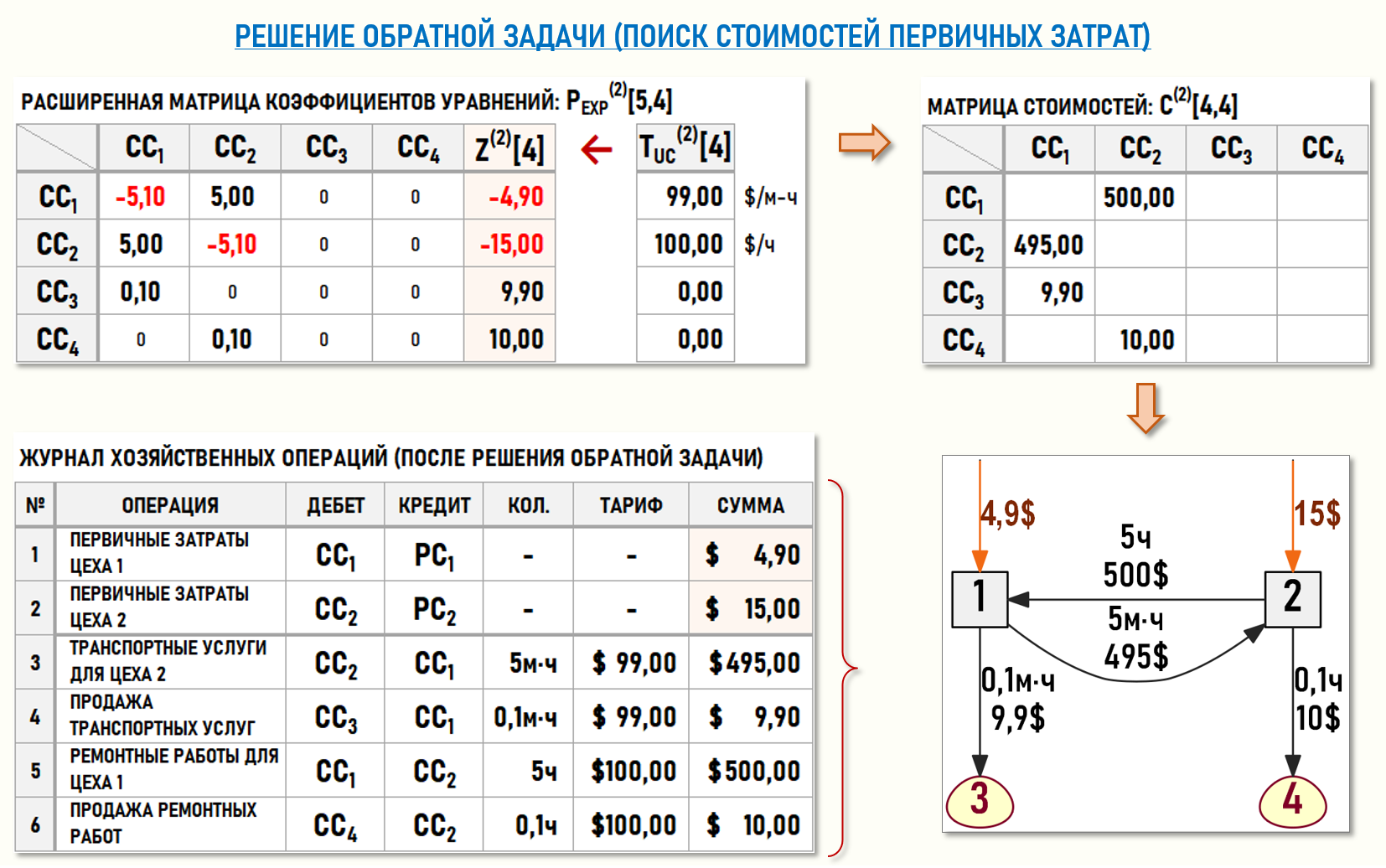
Умножив матрицу коэффициентов уравнений P[4,4] на вектор-столбец тарифов T_UC⁽²⁾[4], получим вектор-столбец правых частей уравнений Z⁽²⁾[4], т.е. определим стоимости первичных затрат Цеха 1 и Цеха 2:

pc₁⁽²⁾=4,90$ – стоимость первичных затрат Цеха 1

pc₂⁽²⁾=15,00$ – стоимость первичных затрат Цеха 2

В нашем примере значения вектора-столбца правых частей уравнений Z⁽²⁾[4] были сформированы только с помощью стоимостей первичных затрат, т.е. стоимости затрат в незавершенном производстве на начало и на конец периода отсутствуют.

Анализ полученных результатов показывает, что уменьшение тарифа t_UC1 на 1% повлекло за собой серьезные изменения стоимостей первичных затрат:

∆pc₁=pc₁⁽²⁾–pc₁⁽¹⁾=4,9$–10$=-5,1$  →  dpc₁=-5,1$/10$=-0,51 (-51%)

∆pc₂=pc₂⁽²⁾–pc₂⁽¹⁾=15$–10$=5$  →  dpc₂=5$/10$=0,50 (+50%)

  

    

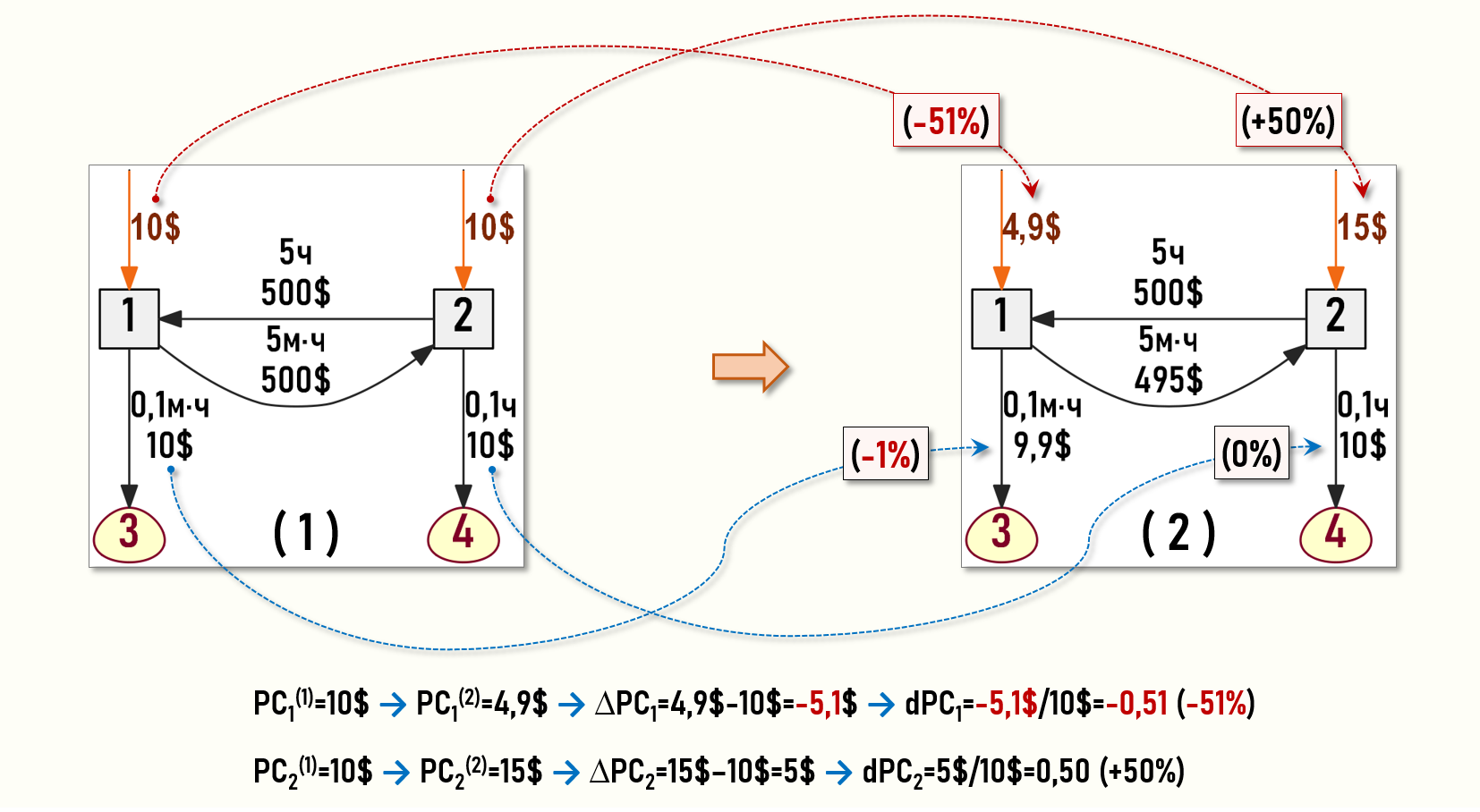
Такое поведение стоимостей первичных затрат pc₁ и pc₂ при незначительном (всего на 1%) изменении величины тарифа t_UC1 вполне можно оценить как невыполнение третьего условия корректности задачи – условия устойчивости решения обратной задачи.

 Действительно, в процессе решения обратной задачи, значение тарифа t_UC1⁽²⁾=99$/м-ч можно рассматривать в качестве ближайшего окружения для базовой величины тарифа t_UC1⁽¹⁾=100$/м-ч.

 Что касается величины pc₁⁽²⁾=4,90$, то это значение уже нельзя считать ближайшим окружением по отношению к базовому значению pc₁⁽¹⁾=10$.

 Подобная ситуация характерна для матриц коэффициентов уравнений P[N_G,N_G] с числом обусловленности Cond(P) много больше единицы (как правило, больше 10²÷10³).

Обусловленность оценивает близость матрицы коэффициентов P[N_G,N_G] к вырожденной, а число обусловленности Cond(A) является количественной оценкой обусловленности. В нашем примере число обусловленности ≈101, такие СЛАУ уже можно считать плохо обусловленными.

 Числом обусловленности матрицы коэффициентов уравнений P[N_G,N_G] называется произведение:

 Cond(P)=║P║║P^-1║

 где:

 ║P║=(Σ_i,jp_i,j²)^½ – евклидова норма матрицы P[N_G,N_G]

 ║P^-1║=(Σ_i,jp^-1_i,j²)^½ – евклидова норма обратной матрицы P^-1[N_G,N_G]

 В данном случае в качестве нормы матрицы использовалась евклидова норма.

 Вывод: Обратные задачи с присущими их решению особенностями только на первый взгляд кажутся чем-то очень далеким от бухгалтерского учета. На самом деле, понимание особенностей решения обратных задач имеет огромное значение для специалистов, занимающихся вопросами микроэкономики, что и было проиллюстрировано рассмотренным в статье примером.