Подмножества соседних центров затрат
Автор: Александр Поляков
В данной статье мы рассмотрим некоторые важные подмножества центров затрат и дуг, используемые при решении задач на Графах затрат. Обратим внимание читателя на тот факт, что данные подмножества действительно используются в алгоритмах решения практических задач на Графах затрат, т.е. материал настоящей статьи не стоит рассматривать в качестве «скучного» теоретизирования на тему, хотя и нужную, но не имеющею особого смысла для практического моделирования. Например, такое важное функциональное свойство любого центра затрат, как схема распределения затрат, требует нахождения для рассматриваемого центра затрат его подмножества соседей-получателей затрат.
Далее будут рассмотрены следующие шесть подмножеств, каждое из которых можно сформировать для любого центра затрат CCi:
ADJV(CCi) – подмножество соседей
ADJVOUT(CCi) – подмножество соседей-получателей затрат
ADJVIN(CCi) – подмножество соседей-источников затрат
ADJE(CCi) – подмножество инцидентных дуг
ADJEOUT(CCi) – подмножество исходящих дуг
ADJEIN(CCi) – подмножество входящих дуг
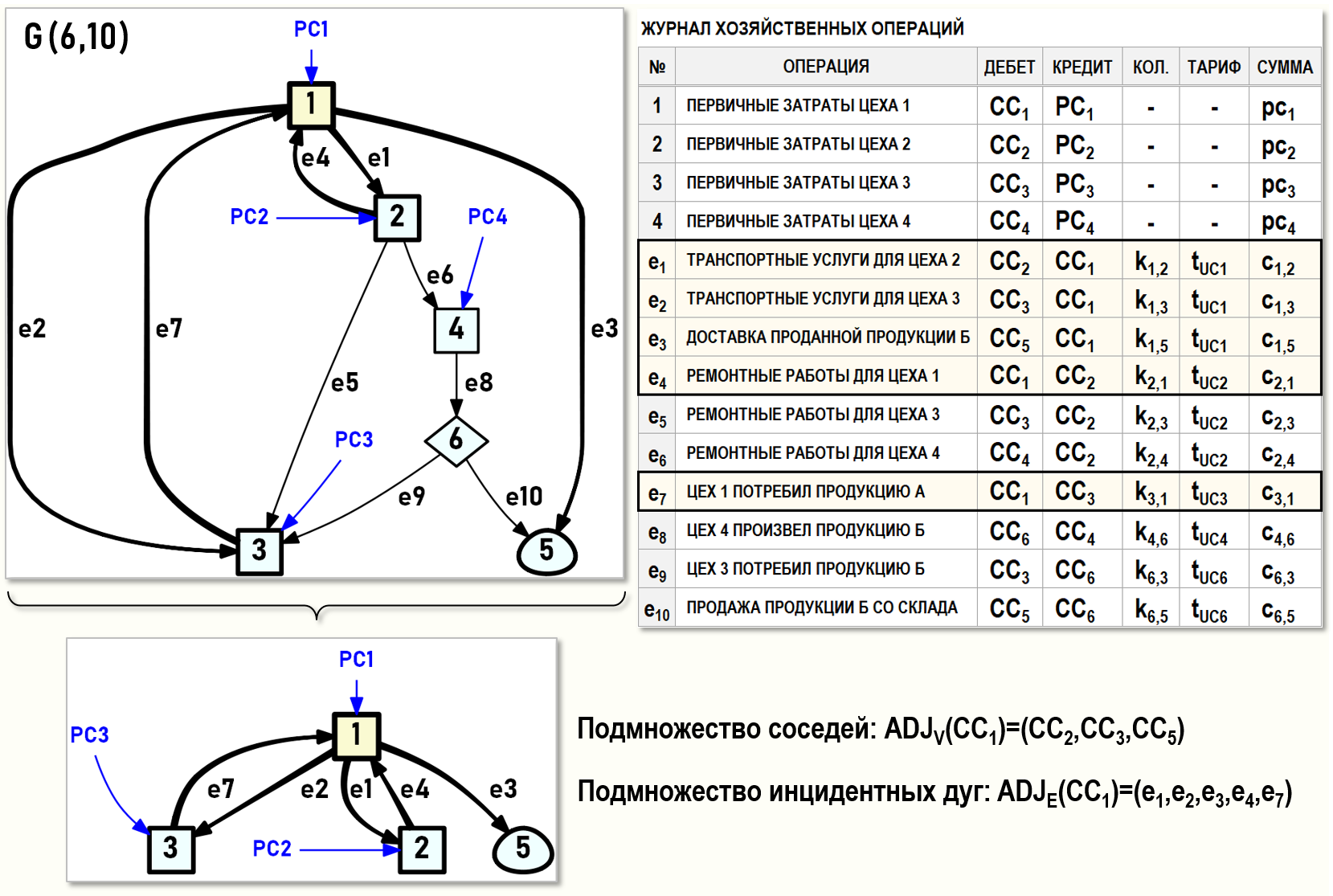
Рассмотрим данные подмножества на примере предприятия, представленного ниже на рисунке Графом затрат G(6,10). Предприятие производит и продает продукцию вида Б, все хозяйственные операции за отчетный период представлены в журнале хозяйственных операций (ЖХО):
Цех 1 (СС1) оказывает транспортные услуги Цеху 2 (СС2), Цеху 3 (СС3) и доставляет проданную продукцию покупателям (СС5).
Цех 2 (СС2) выполняет ремонтные работы для Цеха 1 (СС1), Цеха 3 (СС3) и Цеха 4 (СС4).
Цех 3 (СС3) производит продукцию вида А и передает ее Цеху 1 (СС1).
Цех 4 (СС4) производит продукцию вида Б и помещает ее на Склад предприятия (СС6). Часть продукции со склада продается покупателям (СС5), другая часть продукции передается в Цех 3 (СС3) для производства продукции вида А.
Полная себестоимость проданной продукции вида Б формируется в центре затрат СС5 и складывается из себестоимости продукции вида Б, поступившей со Склада (СС6), и себестоимости транспортных услуг Цеха 1 (СС1) по доставке продукции покупателям.
ПОДМНОЖЕСТВА СОСЕДЕЙ И ИНЦИДЕНТНЫХ ДУГ
Для того, чтобы при решении задач на Графе затрат G(6,10) определить, какие потоки вторичных затрат и откуда получает Цех 1 (СС1), а также – куда он их отдает, можно воспользоваться подмножествами его соседей и инцидентных дуг.
Подмножество соседей центра затрат CC1 формируется центрами затрат, которые связаны с ним инцидентными дугами, т.е. дугами любой направленности, как входящими в центр затрат CC1, так и исходящими из него:
ADJV(CC1)={CC2,CC3,CC5}
NADJ(CC1)=3 – число соседних центров затрат
Подмножество инцидентных дуг центра затрат CC1:
ADJE(CC1)={e1,e2,e3,e4,e7}
DS(CC1)=5 – степень центра затрат CC1, т.е. число инцидентных дуг
В данном случае рассматриваются только потоки вторичных затрат, т.е. дуги, соединяющие между собой пары центров затрат. Технологические дуги, с помощью которых показываются потоки первичных затрат – {pc1,pc2,pc3,pc4} при формировании подмножества инцидентных дуг не учитываются.
ПОДМНОЖЕСТВА СОСЕДЕЙ-ПОЛУЧАТЕЛЕЙ ЗАТРАТ И ИСХОДЯЩИХ ДУГ
Для того, чтобы определить, куда из Цеха 1 (СС1) уходят вторичные затраты, т.е. кому оказываются транспортные услуги, можно воспользоваться подмножествами соседей-получателей затрат и исходящих дуг центра затрат CC1.
Подмножество соседей-получателей затрат формируется центрами затрат, связанными с центром затрат CC1 дугами, исходящими из него:
ADJVOUT(CC1)={CC2,CC3,CC5}
NADJOUT(CC1)=3 – число соседей-получателей затрат
Подмножество исходящих дуг центра затрат CC1:
ADJEOUT(CC1)={e1,e2,e3}
DOUT(CC1)=3 – полустепень исхода CC1, т.е. число исходящих из него дуг
Например, одним из трех этапов выполнения алгоритма R-S-B, лежащего в основе любой схемы распределения затрат, является нахождение подмножества соседей-получателей затрат. Это подмножество указывает, каким соседним центрам затрат отдаются вторичные затраты в процессе выполнения процедуры «закрытия» затрат периода.
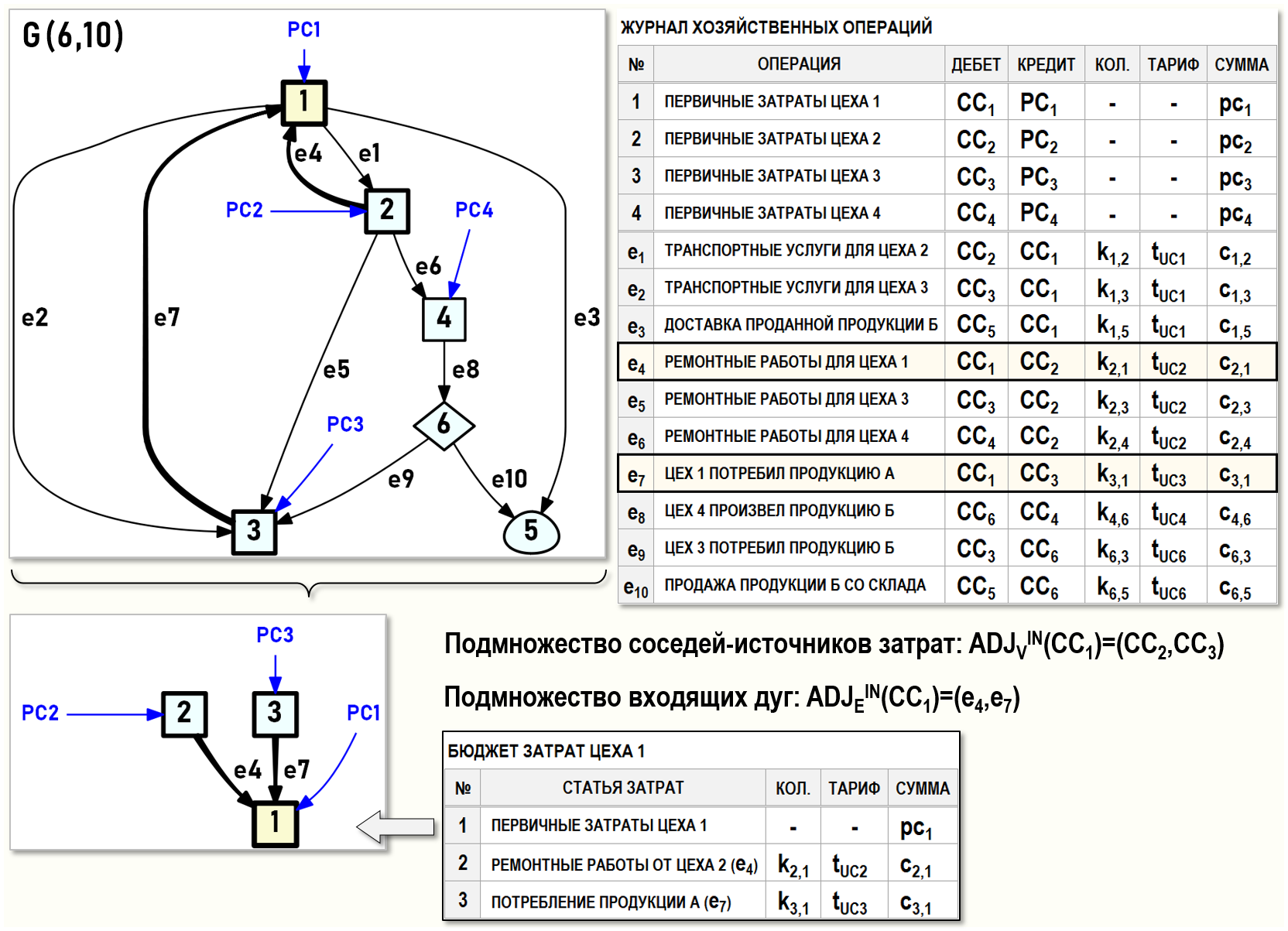
ПОДМНОЖЕСТВА СОСЕДЕЙ-ИСТОЧНИКОВ ЗАТРАТ И ВХОДЯЩИХ ДУГ
Для того, чтобы определить, откуда Цех 1 (СС1) получает вторичные затраты, т.е. откуда он получает продукцию, работы и услуги, можно воспользоваться подмножествами соседей-источников затрат и входящих дуг центра затрат CC1.
Подмножество соседей-источников затрат формируется центрами затрат, связанными с центром затрат CC1 дугами, входящими в него:
ADJVIN(CC1)={CC2,CC3}
NADJIN(CC1)=2 – число соседей-источников затрат
Подмножество входящих дуг центра затрат CC1:
ADJEIN(CC1)={e4,e7}
DIN(CC1)=2 – полустепень захода CC1, т.е. число входящих в него дуг
Например, входящие дуги, т.е. входящие потоки вторичных затрат, участвуют в формировании бюджета затрат Цеха 1 (CC1).