Коэффициенты коммуникабельности центров затрат

    

Автор:  Александр Поляков

 

Рассмотрим коэффициенты, позволяющие количественно оценить, насколько активно центр затрат участвует в процессах распределения вторичных затрат в Графе затрат. Оценивать данную способность центра затрат будем на основе его коммуникабельности, т.е. способности к установлению связей с другими центрами затрат Графа затрат.

Рассмотрим четыре основных коэффициента:

K_V(CC_i) ‒ коэффициент коммуникабельности по центрам затрат 

K_E(CC_i) ‒ коэффициент коммуникабельности по связям 

K_OUT(CC_i) ‒ коэффициент коммуникабельности по выходу

K_IN(CC_i) ‒ коэффициент коммуникабельности по входу

 

Коэффициент коммуникабельности по центрам затрат K_V(CC_i)

 

Значение коэффициента K_V(СС_i) определяет, какая доля из всего числа центров затрат Графа затрат (исключая сам центр затрат СС_i) входит в подмножество его соседей ADJ_V(СС_i):

K_V(CC_i)=N_ADJ(CC_i) / (N_G‒1)

где:

N_ADJ(CC_i) ‒ число соседей центра затрат CC_i 

N_G ‒ порядок Графа затрат 

Диапазон изменения значений коэффициента коммуникабельности по центрам затрат составляет:

K_V(CC_i)=[0..1] или [0%..100%]

Значение K_V(СС_i)=0 (0%) говорит о том, что центр затрат СС_i является изолированным, т.е. не имеет в Графе затрат ни одного соседа, он не получает и не отдает другим центрам затрат потоки вторичных затрат. Однако, это не исключает того, что на входе центра затрат СС_i могут присутствовать потоки первичных затрат.

Значение K_V(СС_i)=1 (100%) говорит о том, что центр затрат СС_i соединен входящими или исходящими дугами со всеми остальными центрами затрат Графа затрат, т.е. центр затрат СС_i можно охарактери­зовать как гиперак­тивный центр затрат. В практическом моделировании подобные центры затрат встречаются крайне редко.

ПРИМЕР:

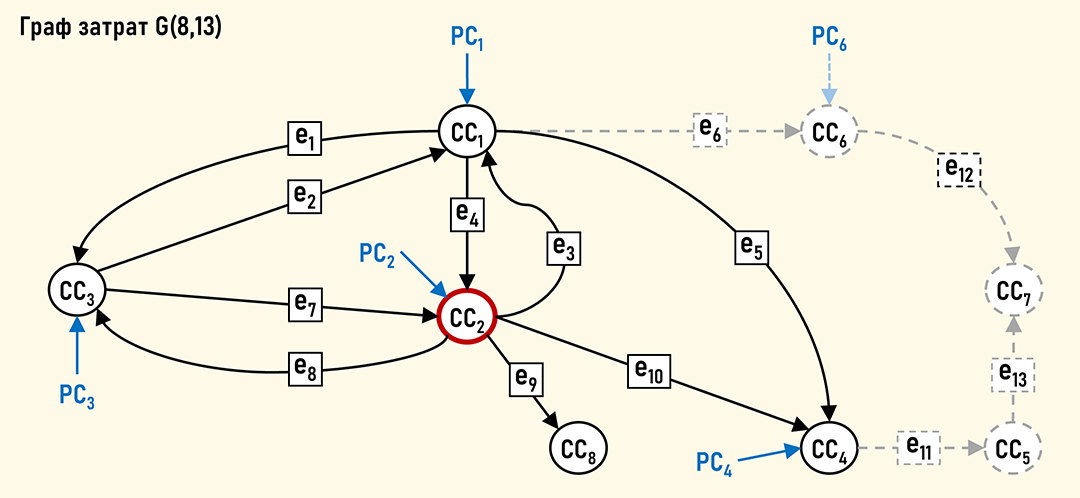
Рассмотрим пример расчета коэффициента коммуникабельности по центрам затрат. Ниже на рисунке представлен Граф затрат G(8,13). Расчет произведем для центра затрат CC₂.

Первое, что необходимо сделать – это найти для центра затрат CC₂ подмножество его соседей ADJ_V(CC₂)={CC₁,CC₃,CC₄,CC₈}. Не входящие в это подмножество центры затрат показаны на рисунке пунктирными линиями.

 

  

Теперь у нас есть значения всех величин, необходимых для расчета коэффициента K_V(CC₂):

N_G=8 ‒ порядок Графа затрат G(8,13)

N_ADJ(CC₂)=4 ‒ число центров затрат в подмножестве ADJ_V(CC₂)

Определим значение коэффициента K_V(CC₂):

K_V(CC₂)=N_ADJ(CC₂) / (N_G‒1)=4 / (8‒1)=0,57 (57%)

Смысл полученного значения заключается в том, что 57% от всех центров затрат Графа затрат G(8,13), за исключением самого CC₂, являются соседями центра затрат CC₂.

Коэффициент коммуникабельности по связям K_E(CC_i)

Значение коэффициента K_E(CC_i) определяет, какая доля из числа дуг Графа затрат инцидентна центру затрат СС_i:

K_E(CC_i)=D_S(CC_i) / N_E

где: 

D_S(CC_i) ‒ степень центра затрат CC_i, т.е. число инцидентных дуг

N_E ‒ число связей Графа затрат G(N_G)  

Диапазон изменения значений коэффициента коммуникабельности по связям составляет:

K_E(CC_i)=[0..1] или [0%..100%] 

Значение K_E(СС_i)=0 (0%) говорит о том, что центр затрат СС_i является изолированным, т.е. не соединен дугой ни с одним из центров затрат Графа затрат. Однако, это не исключает наличия на входе центра затрат СС_i потока первичных затрат.

Значение K_E(СС_i)=1 (100%) говорит о том, что центр затрат СС_i соединен входящими или исходящими дугами со всеми остальными центрами затрат Графа затрат, что на практике встречается крайне редко. 

ПРИМЕР:

Рассчитаем коэффициент коммуникабельности по центрам затрат для центра затрат CC₂. Для этого найдем в Графе затрат G(8,13) подмножество инцидентных дуг ADJ_E(CC₂), а значит и степень D_S(CC₂) центра затрат СС₂:

ADJ_E(CC₂)={e₃,e₄,e₇,e₈,e₉,e₁₀}

D_S(CC₂)=6 ‒ степень центра затрат СС₂

Теперь у нас есть значения всех величин, необходимых для расчета коэффициента K_E(CC₂):

K_E(CC₂)=D_S(CC₂) / N_E=6/13=0,46 (46%) 

Смысл полученного значения заключается в том, что 46% от всех дуг Графа затрат G(8,13) являются инцидентными центру затрат СС₂. 

 

Коэффициент коммуникабельности по выходу K_OUT(CC₂)

 

Значение коэффициента K_OUT(CC_i) определяет, какую долю из числа всех дуг Графа затрат составляют дуги, исходящие из центра затрат СС_i:

K_OUT(CC_i)=D_OUT(CC_i) / N_E

где: 

D_OUT(CC_i) ‒ полустепень исхода центра затрат CC_i, т.е. число исходящих из него дуг

N_E ‒ число связей Графа затрат G(N_G) 

Диапазон изменения значений коэффициента коммуникабельности по выходу составляет:

K_OUT(CC_i)=[0..1] или [0%..100%] 

Значение K_OUT(СС_i)=0 (0%) говорит о том, что центр затрат СС_i не отдает потоки вторичных затрат другим центрам затрат Графа затрат. Центр затрат с таким значением коэффициента K_OUT(СС_i) может быть:

изолированным центром затрат

стоком

Значение K_OUT(СС_i)=1 (100%) говорит о том, что центр затрат СС_i соединен исходящими дугами со всеми остальными центрами затрат Графа затрат (кроме изолированных центров затрат), т.е. отдает элементарные потоки вторичных затрат всем остальным центрам затрат Графа затрат. В практическом моделировании это маловероятный случай. 

ПРИМЕР:

Рассчитаем коэффициент коммуникабельности по выходу для центра затрат CC₂. Для этого найдем в Графе затрат G(8,13) подмножество исходящих дуг ADJ_E^OUT(CC₂), а значит и полустепень исхода D_OUT(CC₂) центра затрат СС₂:

ADJ_E^OUT(CC₂)={e₃,e₈,e₉,e₁₀}

D_OUT(CC₂)=4 

Теперь у нас есть значения всех величин, необходимых для расчета коэффициента K_OUT(CC₂):

K_OUT(CC₂)=D_OUT(CC₂) / N_E=4 / 13=0,31 (31%)

Смысл полученного значения заключается в том, что 31% от всех дуг Графа затрат G(8,13) являются исходящими из центра затрат СС₂.

 

Коэффициент коммуникабельности по входу K_IN(CC_i)

 

Значение коэффициента K_IN(CC_i) определяет, какую долю из всего числа связей Графа затрат составляют дуги, поступающие на вход центра затрат СС_i:  

K_IN(CC_i)=D_IN(CC_i) / N_E

где: 

D_IN(CC_i) ‒ полустепень захода центра затрат CC_i, т.е. число входящих в него дуг

N_E ‒ число связей Графа затрат G(N_G) 

Диапазон изменения значений коэффициента коммуникабельности по входу составляет:

K_IN(CC_i)=[0..1] или [0%..100%] 

Значение K_IN(СС_i)=0 (0%) говорит о том, что центр затрат СС_i не получает элементарные потоки вторичных затрат от других центров затрат Графа затрат. Центр затрат с таким значением коэффициента K_IN(СС_i) может быть:

изолированным центром затрат

истоком

Оба варианта не исключают наличия на входе центра затрат CC_i потока первичных затрат.

Значение K_IN(СС_i)=1 (100%) говорит о том, что центр затрат СС_i соединен входящими дугами со всеми остальными центрами затрат Графа затрат (кроме изолированных центров затрат), т.е. получает элементарные потоки вторичных затрат от всех остальных центров затрат Графа затрат. В практическом моделировании это маловероятный случай. 

ПРИМЕР:

Рассчитаем коэффициент коммуникабельности по входу для центра затрат CC₂. Для этого найдем в Графе затрат G(8,13) подмножество входящих дуг ADJ_E^IN(CC₂), а значит и полустепень захода D_IN(CC₂) центра затрат СС₂:

ADJ_E^IN(CC₂)={e₄,e₇}

D_IN(CC₂)=2

Теперь у нас есть значения всех величин, необходимых для расчета коэффициента K_IN(CC₂):

K_IN(CC₂)=D_IN(CC₂) / N_E=2 / 13=0,15 (15%) ‒ определяем значение коэффициента

Смысл полученного значения заключается в том, что 20% от всех дуг Графа затрат G(8,13) являются входящими в центр затрат СС₂.

Следует иметь в виду, что состав коэффициентов коммуникабельности в случае необходимости можно расширить. Например, можно использовать коэффициенты коммуникабельности по различным классам центров затрат, классам связей и т.п.