Метод весовых коэффициентов (выпуск нескольких видов продукции)
Автор: Александр Поляков
В данной статье мы рассмотрим вопрос, который от специалистов по расчету себестоимости можно услышать не просто часто, а очень часто. Формулируется он обычно так – у нас на предприятии есть подразделения, которые производят несколько видов продукции в одном и том же периоде, или одновременно производят продукцию и оказывают услуги или выполняют работы. Как рассчитать себестоимость в этом случае?
С подобной ситуацией рано или поздно сталкивается каждый специалист по расчету себестоимости, поэтому необходимо выяснить, почему возникают такие ситуации, когда от них можно уйти, а когда уйти не получится, и что в этом случае делать.
Напомним, что в Графе затрат любой центр затрат является для пользователя модели «черным ящиком», внутренние процессы которого пользователю недоступны для наблюдения. Пользователь не может увидеть, каким образом внутри центра затрат происходит превращение входящих потоков затрат в исходящие потоки затрат, т.е. как делится стоимость входящих потоков затрат между исходящими потоками затрат, которые относятся к разным видам продукции, работ и услуг.
Пользователь видит только, что на вход центра затрат зашли потоки первичных и вторичных затрат, а на выходе появились потоки вторичных затрат, относящиеся к разным видам продукции. В математической модели для расчета себестоимости стоимости этих исходящих потоков вторичных затрат определяются с помощью единиц калькуляции разного вида. И эти разные единицы калькуляции имеют разные стоимости (тарифы). Как это можно объяснить?
Здесь можно предложить такую наглядную аналогию. Возьмем непрозрачную емкость с двумя выводными трубками, на рисунке в качестве такой емкости показан чайник с двумя носиками, и нальем в него жидкости трех цветов – красного, зеленого и синего. А потом нальем из одного носика в чашку жидкость розового цвета, а из другого носика в другую чашку жидкость фиолетового цвета. Как такое может быть?
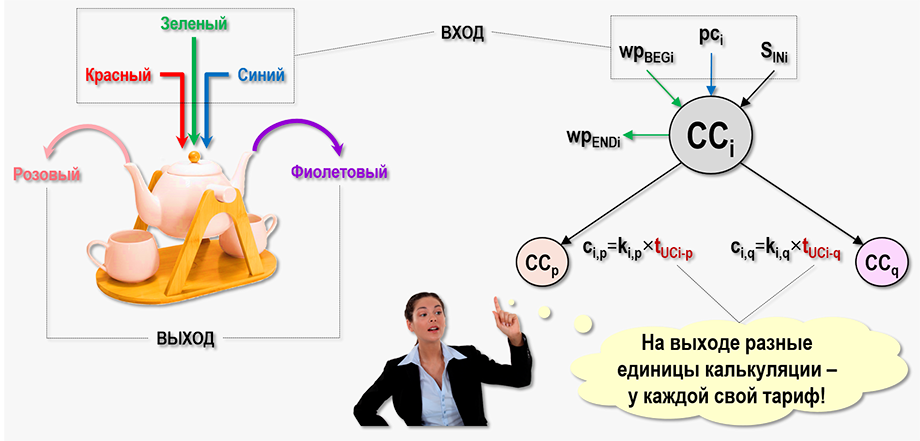
Смешанные в определенных пропорциях жидкости этих трех цветов могут дать на выходе любой заранее заданный цвет, но у нас получилось два разных цвета, а жидкости мы наливали в один общий чайник. Это означает, что внутри чайника произошли какие-то более сложные процессы, чем простое перемешивание жидкостей трех базовых цветов. Возможно внутри чайника присутствует система перегородок, ограничивающих полости, в которых жидкости перемешиваются в разных пропорциях, образуя разные цвета, но в виду непрозрачности материала, из которого сделан чайник, не удается увидеть, что происходит внутри. Внешнему наблюдателю виден только конечный результат смешивания жидкостей, когда из одного носика выливается розовая жидкость, а из другого – фиолетовая. Если же нужно узнать, как получился такой результат, то придется получить дополнительную информацию, например, заглянуть внутрь чайника.
Такая же ситуация наблюдается и с центрами затрат в Графе затрат. Выше на рисунке пользователь модели видит на выходе центра затрат CCi потоки затрат, соответствующие разным видам продукции, работ или услуг. На вход центра затрат CCp уходит поток затрат, стоимость которого рассчитывается с помощью тарифа tUCi-p, а на вход центра затрат CCq уходит поток затрат, стоимость которого рассчитывается с помощью тарифа tUCi-q.
Для того, чтобы понять, как на выходе центра затрат получаются разные тарифы для разных видов продукции, работ или услуг, пользователю необходимо заглянуть внутрь центра затрат, посмотреть на его внутренние потоки затрат. А это означает, что данная модель просто не соответствует ожиданиям пользователя, она слишком приблизительная для тех задач, которые он хочет решать с ее помощью. В этом случае желательно построить более подробную модель, в которой таких вопросов у пользователя возникать не будет.
Например, можно разделить центр затрат на несколько центров затрат и организовать между ними движение потоков затрат так же, как это происходило внутри исходного центра затрат, но было скрыто от пользователя модели. Если вопросы не исчезнут, то путем подобных итераций можно уточнять модель до тех пор, пока пользователь не решит, что для решения его задачи дальше уже нет нужды в получении более подробного Графа затрат. Основная задача – построить модель так, чтобы на выходе каждого центра затрат был бы только один вид единицы калькуляции. Это необходимое условие для решения задач на Графе затрат, т.к. только в этом случае эффективно начнут работать уравнения баланса затрат для расчета себестоимости.
На практике часто по тем или иным причинам, зависящим или не зависящим от разработчика модели, в Графе затрат все-таки остаются отдельные центры затрат, на выходе которых существуют единицы калькуляции разного вида. Например, когда из полиметаллической руды, то есть руды, одновременно содержащей несколько видов драгоценных металлов, пытаются выделить, например, золото и серебро, то довольно долго эти два металла идут по цепочке технологического процесса вместе, как составляющие одного концентрата. А учет драгоценных металлов производится на каждом переделе не в тоннах руды или концентрата, а в граммах, содержащихся в них драгоценных металлов, т.к. происходит постоянное измерение их содержания в концентрате. Получается, что на выходе отдельных переделов золото и серебро идут вместе, а затраты на их получение необходимо считать раздельно. Такая же ситуация возникает и с попутным природным газом, который выходит на поверхность одновременно с добычей нефти, и еще в ряде подобных случаев.
Практика моделирования предусматривает еще одну ситуацию, при которой в Графе затрат могут быть использованы центры затрат, выпускающие несколько видов продукции, работ и услуг. Данная ситуация возникает тогда, когда технологический процесс предприятия позволяет выбрать на выходе каждого центра затрат только один вид единицы калькуляции, но(!) разработчик Графа затрат по каким-либо причинам не использует эту возможность. Часто это обусловлено просто нежеланием пользователя модели увеличивать порядок Графа затрат, т.к. это повышает трудоемкость учета затрат, т.е. увеличивает рабочую нагрузку на пользователей системы учета. Действительно, в этом случае может потребоваться ввод в автоматизированную систему учета большого объема дополнительных аналитических данных. Кроме того, становится сложнее контролировать логическую целостность модели, труднее разбираться с ошибками, возникающими во время проведения процедуры распределения потоков вторичных затрат.
Отчасти, подобное поведение разработчиков модели можно оправдать тем, что увеличение порядка Графа затрат требует изменения системы делопроизводства, т.к. первичные учетные данные придется в этом случае вводить в автоматизированную систему учета для возросшего числа центров затрат. Иногда это может явиться непреодолимым препятствием для успешного внедрения спроектированного Графа затрат и заставить разработчика пересмотреть топологию Графа затрат в сторону ее упрощения.
В общем, существуют ситуации, когда не удается (или экономически нецелесообразно) построить очень подробные модели предприятий для расчета себестоимости. Что в этом случае делать? И вот здесь может помочь алгоритм A-W-C, называемый также методом весовых коэффициентов, который мы и рассмотрим далее на примере.
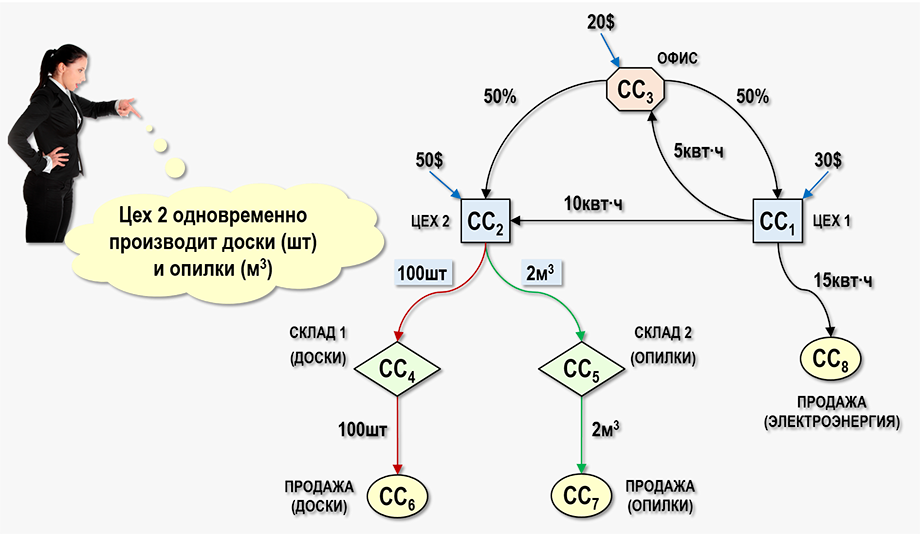
В качестве примера рассмотрим обычную лесопилку, цех 2 которой производит доски. Как известно, производство досок сопровождается получением опилок. Лесопилка имеет свою дизельную электростанцию (цех 1), которая снабжает электроэнергией цех 2, офис, в котором работает административный персонал, также часть электроэнергии продается сторонним потребителям.
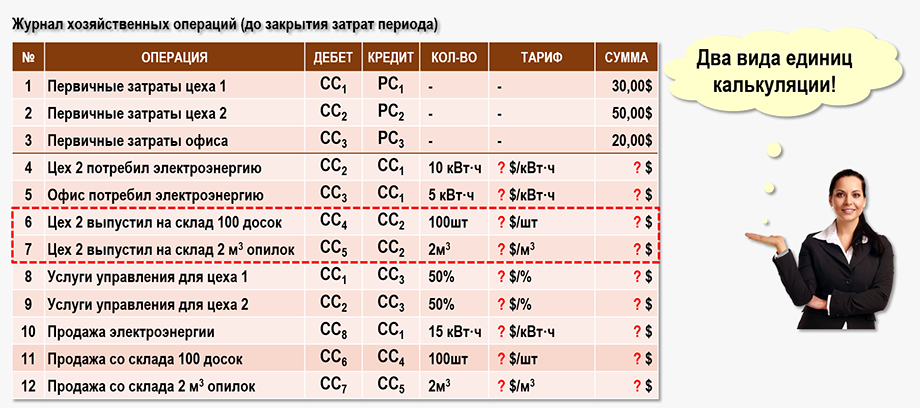
Журнал хозяйственных операций до проведения процедуры распределения вторичных затрат (закрытия затрат) имеет следующий вид:
В общем случае разработчик модели должен рассматривать доски и опилки как равноправные виды продукции, для которых надо рассчитать себестоимость. А далее руководитель предприятия сам решит, что он будет делать с этой продукцией – считать ли опилки ненужными отходами или такой же продукцией, как и доски. В конце концов все определяется уровнем развития технологий. Сегодня опилки являются отходами производства, а завтра – опилки уже становятся ценным сырьем для производства топливных брикетов. Поэтому доски и опилки будем считать видами продукции, производство которых цехом 2 по понятным причинам происходит одновременно. Каждый вид продукции поступает на свой склад и далее продается покупателям.
На выходе центра затрат CC2 мы видим единицы калькуляции двух видов – доски, измеряемые в штуках (100шт), и опилки, измеряемые в кубических метрах (2 м3). А нам нужно получить только один вид единицы калькуляции. И для этого можно воспользоваться методом весовых коэффициентов.
Идея этого метода довольна проста и заключается в том, что с помощью разного рода дополнительной информации нужно понять, можно ли найти какую-то общую для досок и опилок единицу измерения. В теории Графов затрат такая обобщенная единица измерения получила название условной единицы калькуляции. Ее применение позволяет составить уравнение баланса затрат для центра затрат, на выходе которого присутствуют несколько видов исходных единиц калькуляции. Здесь многое зависит от того, насколько хорошо разработчик модели знаком с тонкостями производственного процесса, так как это может позволить подобрать наиболее подходящий вид условной единицы калькуляции. Надо понимать, что это всегда поиск наилучшего приближения к реальной ситуации из некоторого спектра возможных альтернатив и пользователь может это сделать либо лучше, либо хуже. Все определяется тем, как разработчик видит моделируемую ситуацию.
Обсудим, какую условную единицу можно выбрать для нашего примера. Какая у нас есть дополнительная информация? Например, мы знаем, что и доски, и опилки изготовлены из сосны, а ее плотность известна (~0,5 тн/м3). Эта информация позволяет в качестве условной единицы калькуляции выбрать единицу массы (1 тн) досок и опилок в предположении о том, что опилки на складе плотно спрессованы, иначе их плотность будет значительно меньше плотности цельного куска сосны. Конечно, это определенное допущение, но метод весовых коэффициентов лишь в каком-то приближении позволяет привести к единой единице измерения разные виды продукции, работ или услуг.
Далее рассчитаем массу одной доски и 1-го кубометра опилок, это и будут весовые коэффициенты, позволяющие пересчитывать исходные единицы калькуляции в условные единицы калькуляции:
КW1=0,2м×0,2м×6м×0,5тн/м3=0,12 тн
КW2=1м3×0,5тн/м3=0,5 тн
где:
0,2м – высота и ширина доски
6м – длина доски
Полученные весовые коэффициенты показывают, на какое значение необходимо умножить количество исходных единиц калькуляции (штуки и кубометры) для того, чтобы перейти к значениям в условных единицах калькуляции (тонны). Рассчитаем новые значения исходных коэффициентов k2,4 и k2,5:
k2,4 NEW=k2,4×KW1=100×0,12=12 тн – соответствует 100-та доскам
k2,5 NEW=k2,5×KW2=2×0,5=1 тн – соответствует 2 м3 опилок
Покажем полученные значения на Графе затрат:
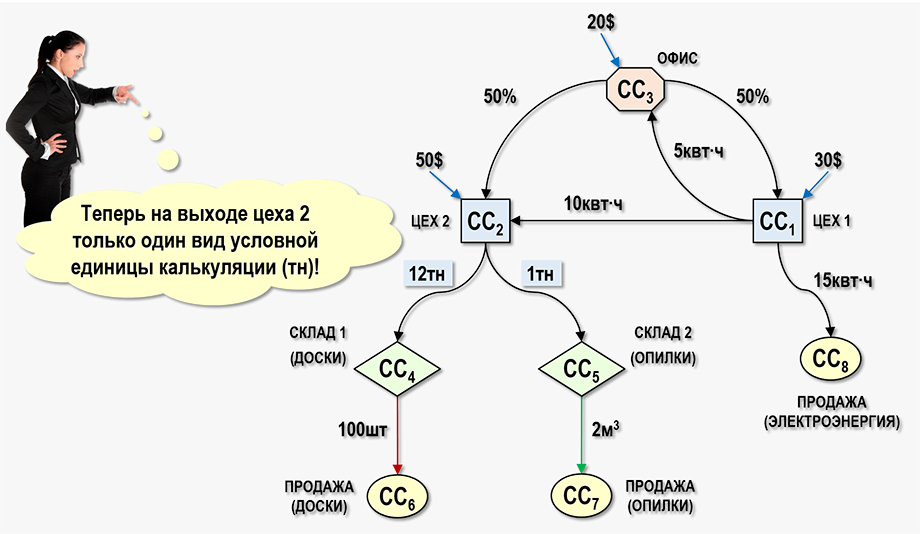
Посмотрим также, как выглядят расширенные матрицы исходных коэффициентов – до и после выбора вида условной единицы калькуляции:
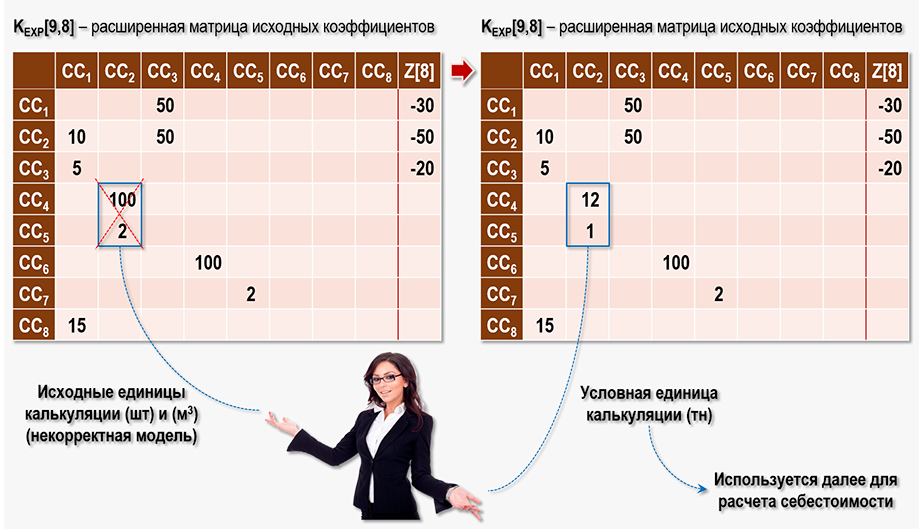
Изначально на выходе второго центра затрат у нас было k2,4=100 досок и k2,5=2 м3 опилок. Теперь на выходе второго центра затрат k2,4 NEW=12 тн досок и k2,5 NEW=1 тн опилок.
Все остальные значения исходных коэффициентов остались без изменений. Причем, возникла интересная ситуация. На входе четвертого и пятого центров затрат, а это продукция на складе, продукция измеряется в тоннах. А на выходах этих центров затрат продукция измеряется в штуках и кубометрах. То есть на склады поступают доски и опилки, измеряемые в условных единицах калькуляции (тн), а уходят со склада доски в штуках и опилки в кубометрах. Но эта подмена единиц калькуляции действует только на время расчета себестоимости, после проведения которого необходимо опять перейти к изначальным единицам калькуляции – штукам и кубометрам.
Расширенная матрица исходных коэффициентов полностью определяет СЛАУ для расчета стоимости потоков затрат. Как решать СЛАУ, можно посмотреть здесь.
Также можно скачать таблицы Microsoft Excel с решением СЛАУ для рассматриваемого примера. Результаты расчета себестоимости представим с помощью следующего Графа затрат:
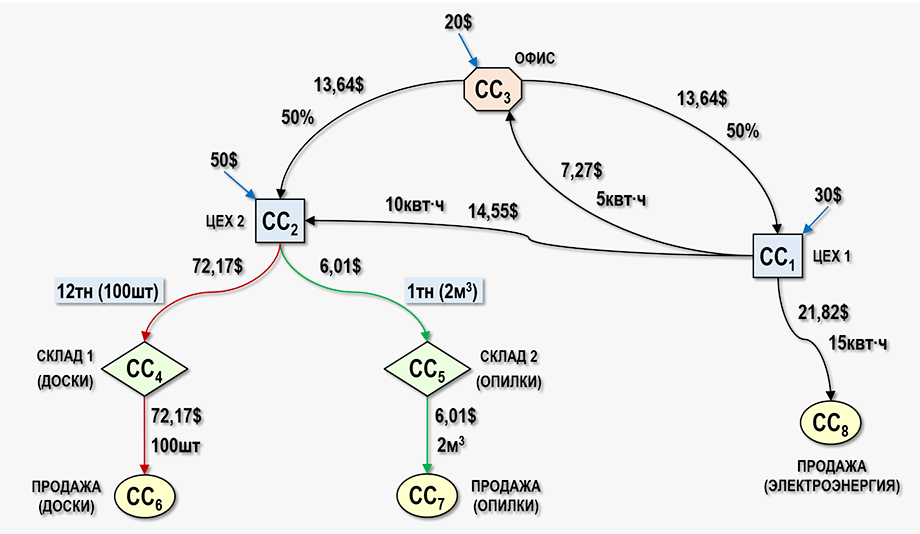
В результате решения СЛАУ (см. таблицы Microsoft Excel) были найдены следующие значения тарифов:
tUC1=1,4545 $/кВт·ч – себестоимость 1 кВт·ч электроэнергии
tUC2=6,0140 $/тн – себестоимость условной единицы калькуляции
tUC3=0,2727 $/% – себестоимость 1 % услуг управления
tUC4=0,7217 $/шт – себестоимость 1-ной доски
tUC5=3,0070 $/м3 – себестоимость 1 м3 опилок
Далее нужно с помощью весовых коэффициентов KW1 и KW2 пересчитать значение тарифа tUC2 для исходных единиц калькуляции – одной доски и 1 м3 опилок:
tUC2-Д=tUC2×KW1=6,0140×0,12=0,7217 $/шт – себестоимость одной доски
tUC2-О=tUC2×KW2=6,0140×0,5=3,0070 $/м3 – себестоимость 1 м3 опилок
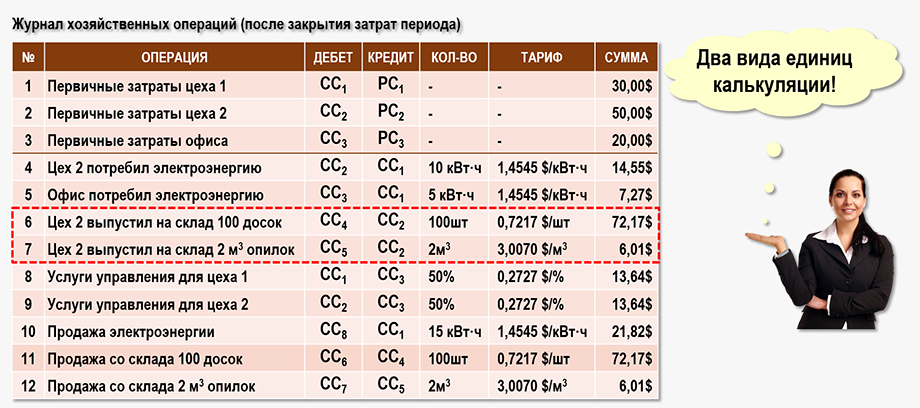
Журнал хозяйственных операций после проведения процедуры распределения вторичных затрат (закрытия затрат) примет следующий вид: