Факторный анализ себестоимости. Пример 1
Автор: Александр Поляков
В настоящее время анализ себестоимости часто проводится (если вообще проводится) с помощью довольно приближенных и весьма простых математических формул исходя из предположения о том, что предприятие представляет собой некий «черный ящик», хозяйственные процессы внутри которого слишком «сложны», а потому как-бы «недоступны» исследователю для непосредственного наблюдения. Такой подход, безусловно, тоже имеет право на существование, но также следует понимать, что перемещение учетных процессов в киберпространство позволяет использовать для этой цели и более прогрессивные технологии расчета и анализа себестоимости.
В данной статье будут рассмотрены некоторые особенности использования Графов затрат для проведения факторного анализа себестоимости на примере небольшого производственного предприятия. Для лучшего понимания материала статьи можно скачать матричную модель, реализованную с помощью связанных таблиц Microsoft Excel, а также ознакомиться с материалом статьи, в которой подробно рассмотрена процедура составления и решения СЛАУ для расчета себестоимости.
Матричная модель для анализа себестоимости
Результаты анализа себестоимости
Обсуждение полученных результатов
УСЛОВИЯ ЗАДАЧИ (↑)
Предприятие в выбранном для анализа периоде осуществляет два вида деятельности:
оказывает (продает) транспортные услуги
выполняет (продает) ремонтные работы
Журнал хозяйственных операций (ЖХО) предприятия для анализируемого периода имеет следующий вид:
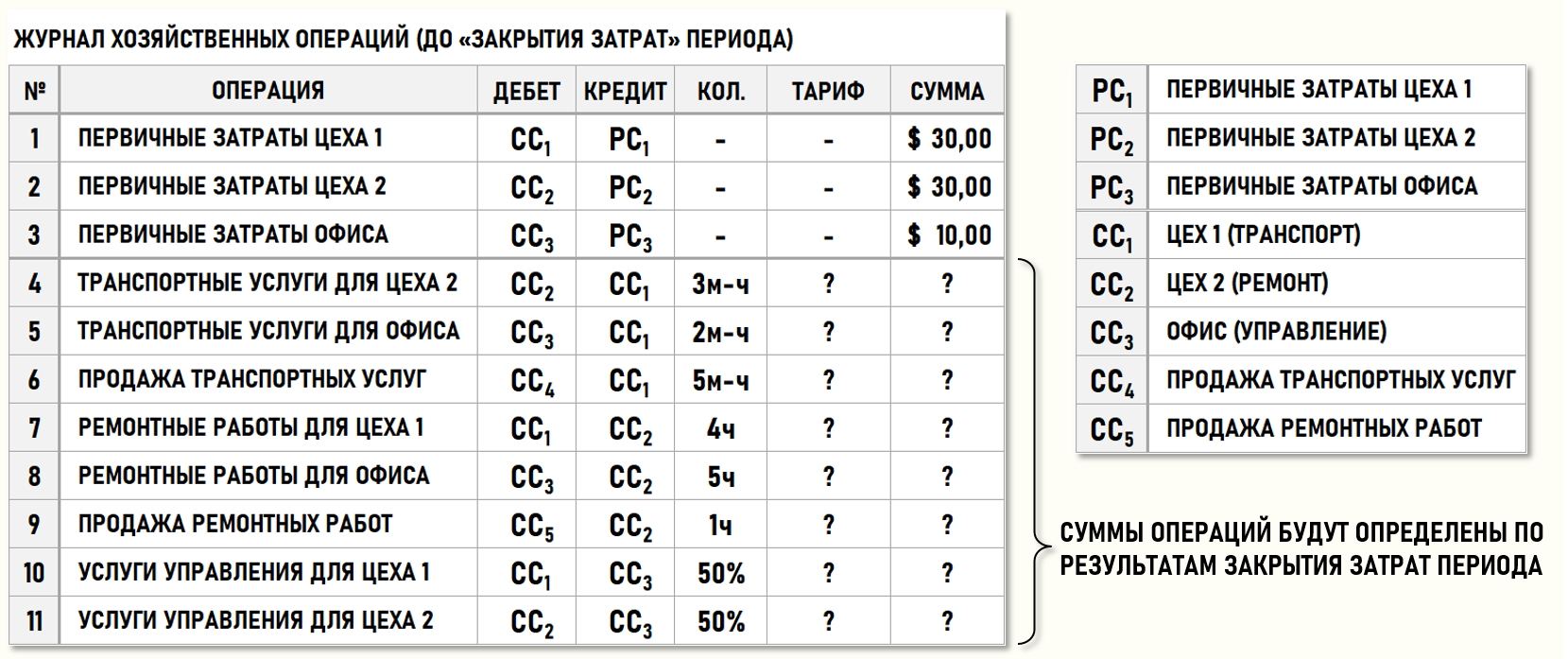
Изображенный на рисунке ЖХО можно рассматривать как табличную форму представления множества хозяйственных операций предприятий в рассматриваемом периоде, но для наглядности можно представить множество хозяйственных операций и в геометрической форме, т.е. в виде рисунка.
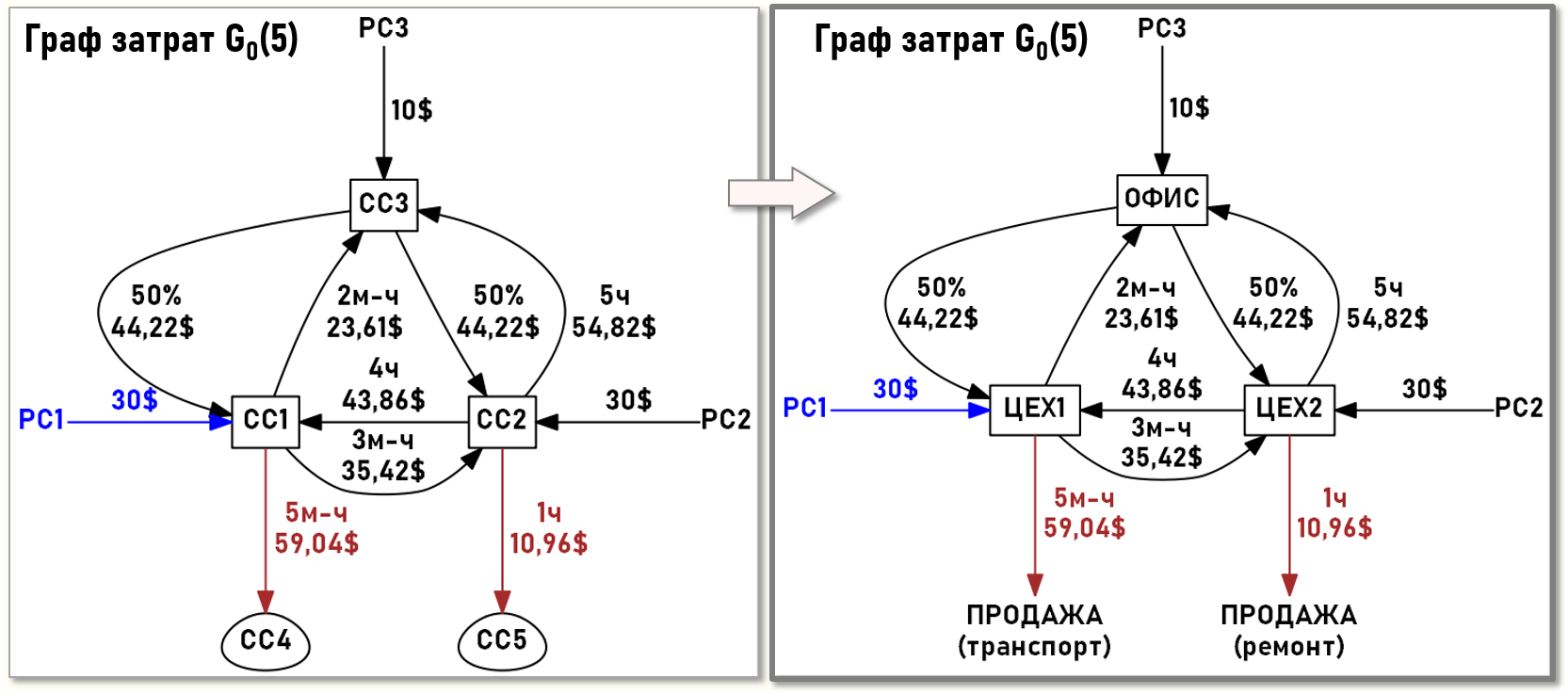
Ниже показаны два варианта Графа затрат для рассматриваемого примера. Слева на рисунке наименования узлов орграфа соответствуют названиям подразделений предприятия, также схематично показаны потоки затрат, формирующие себестоимость проданных транспортных услуг и ремонтных работ. Справа показан этот же орграф, но для наименования узлов используется аббревиатура «CCi» (по первым буквам Cost Centre). Этот вариант представления орграфа более компактен и удобен для использования в расчетах себестоимости, поэтому далее мы будем использовать именно его:
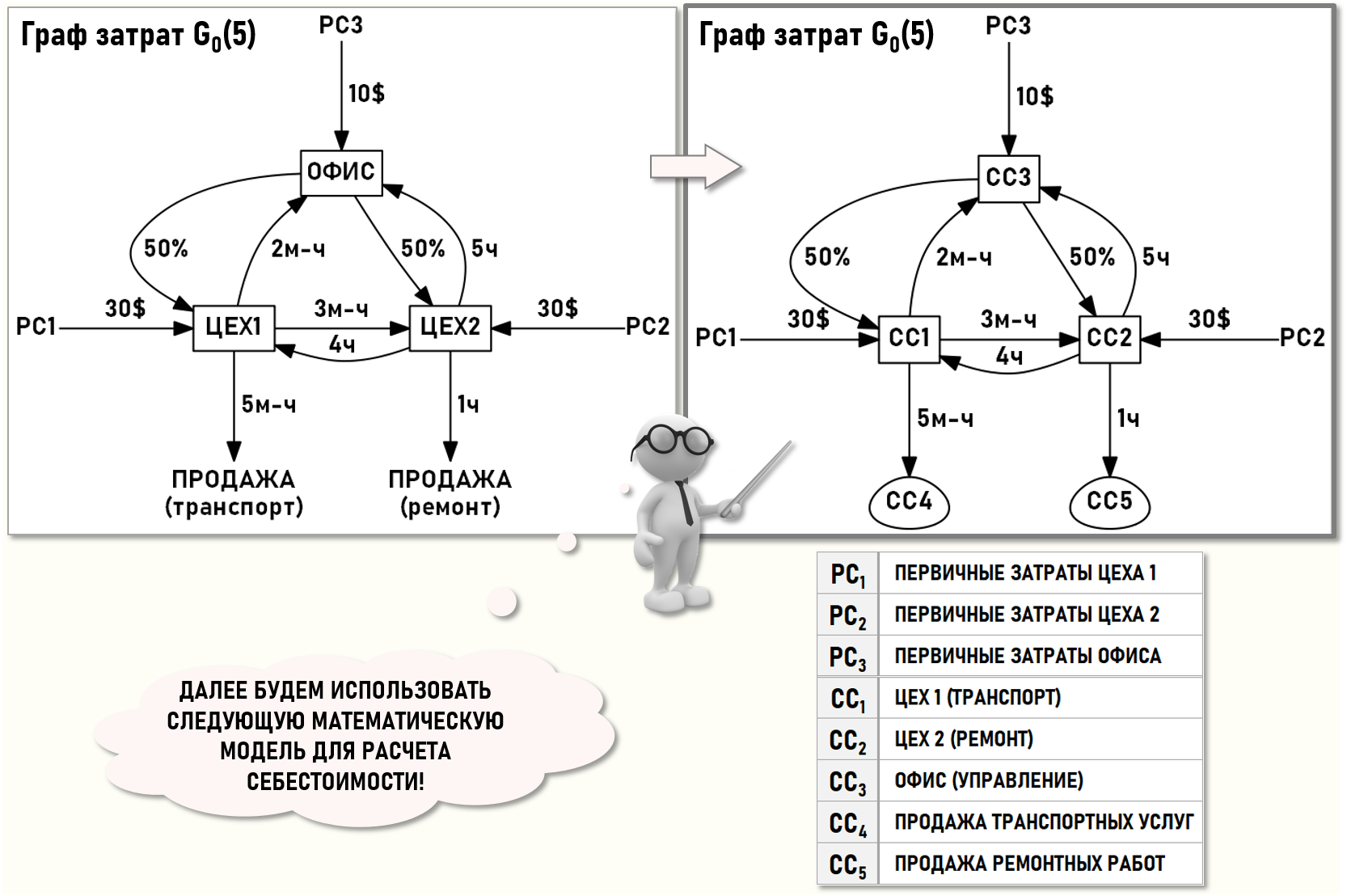
Цех 1 (СС1) оказывает транспортные услуги Цеху 2 и Офису, а также продает их сторонним контрагентам. Объемы транспортных услуг измеряются в машино-часах. Себестоимость проданных транспортных услуг формируется на входе центра затрат CC4.
Цех 2 (СС2) выполняет ремонтные работы для Цеха 1 и Офиса, а также для сторонних контрагентов. Объемы ремонтных работ измеряются в часах. Себестоимость проданных ремонтных работ формируется на входе центра затрат CC5.
В офисе (СС3) сосредоточен административный персонал предприятия. Положением об учетной политике предприятия предусмотрено, что распределение стоимости услуг управления производится пропорционально стоимостям первичных затрат, полученным в анализируемом периоде Цехом 1 и Цехом 2.
Забегая вперед отметим (спойлер), что выбор такого весьма популярного сейчас способа распределения затрат на управление нельзя признать корректным. Но поскольку этот способ (и аналогичные ему) используются в практической работе специалистами по расчету себестоимости, мы рассмотрим его в статье и обсудим возможные последствия его применения.
ЧТО БУДЕМ ИССЛЕДОВАТЬ? (↑)
Стоимости первичных затрат подразделений предприятия в анализируемом периоде составили:
pc1=30$ – первичные затраты Цеха 1 (базовый сценарий)
pc2=30$ – первичные затраты Цеха 2
pc3=10$ – первичные затраты Офиса
Предположим, что для целей финансового планирования необходимо рассмотреть несколько сценариев финансирования деятельности Цеха 1, для чего нужно рассчитать предполагаемые значения себестоимостей проданных транспортных услуг и ремонтных работ в случае, когда стоимость первичных затрат Цеха 1 будет изменяться в диапазоне от 30$ до 45$, т.е. при 50%-ных отклонениях от базового сценария (pc1=30$) как в сторону увеличения, так и в сторону уменьшения стоимости первичных затрат Цеха 1.
Другими словами, в процессе проведения процедуры финансового планирования необходимо рассчитать себестоимость (закрыть затраты периода) для нескольких значений первичных затрат Цеха 1 из диапазона:
pc1=[15$..45$]
Шаг расчета выберем Δpc1=5$, т.е. расчет необходимо выполнить 7 раз.
Таким образом, задачу можно сформулировать следующим образом – необходимо определить характер поведения целевых показателей: себестоимости проданных транспортных услуг (SIN4) и себестоимости проданных ремонтных работ (SIN5) при изменении значений влияющего фактора (pc1) в диапазоне [15$..45$] с шагом Δpc1=5$.
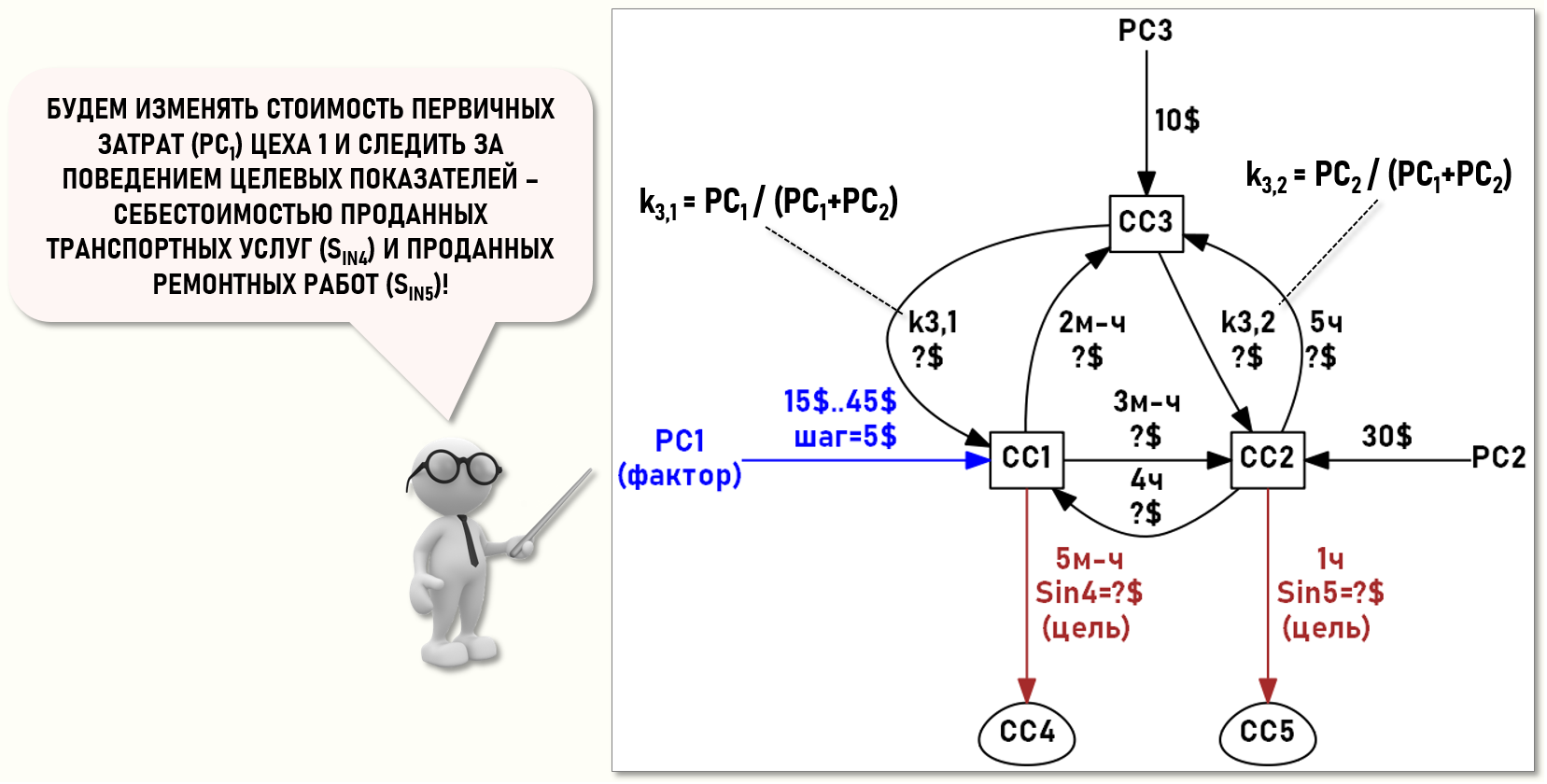
МАТРИЧНАЯ МОДЕЛЬ ДЛЯ АНАЛИЗА СЕБЕСТОИМОСТИ (↑)
Для решения поставленной задачи построим в Microsoft Excel математическую модель в виде системы связанных таблиц (скачать), позволяющих определять значения целевых показателей SIN4 и SIN5 при изменении значения влияющего фактора pc1.
Как известно, главной задачей при расчете себестоимости является формирование расширенной матрицы исходных коэффициентов, которая полностью определяет СЛАУ для расчета себестоимости. Если данная матрица сформирована, то далее остается просто выполнить ряд «технических» вычислительных операций по поиску решения СЛАУ с целью определения тарифов. В нашей задаче расширенная матрица исходных коэффициентов KEXP[6,5] для базового сценария хозяйственной деятельности предприятия имеет следующий вид:

Как видим, в нашей модели любые изменения стоимости первичных затрат pc1 в ячейке J3 влияют на значения исходных коэффициентов k3,1 и k3,2 в ячейках E3 и E4 соответственно, что определяется требованиями Положения об учетной политике предприятия в части распределения управленческих затрат на выходе центра затрат CC3.
Процедуру решения СЛАУ можно посмотреть в таблицах Microsoft Excel, а мы сразу представим результаты расчета для базового сценария хозяйственной деятельности предприятия – значения тарифов tUCi и матрицу стоимостей C[5,5]. В ячейках C37 и D38 содержатся значения целевых показателей SIN4 и SIN5 соответственно:

Получив значения тарифов и стоимостей затрат, можно заполнить ЖХО для базового сценария хозяйственной деятельности предприятия:
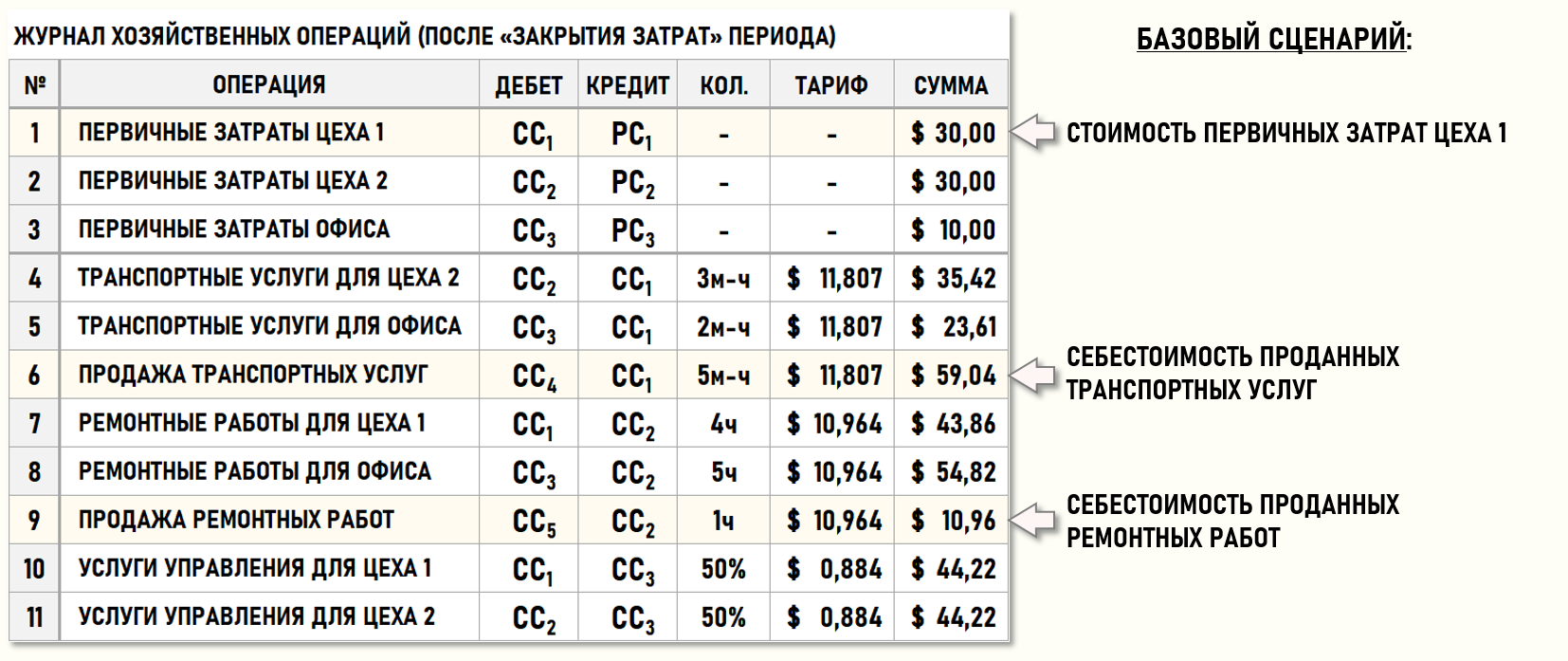
Также представим результаты расчета для базового сценария в геометрической форме:
Таким образом, мы построили систему связанных таблиц Microsoft Excel, позволяющую рассчитать значения целевых показателей SIN4 и SIN5 при изменении значения влияющего фактора pc1, и теперь можно приступать к анализу себестоимости.
РЕЗУЛЬТАТЫ АНАЛИЗА СЕБЕСТОИМОСТИ (↑)
Изменяя стоимость первичных затрат pc1 (ячейка J3) в диапазоне [15$..45$] с шагом 5$, произведем решение СЛАУ в таблицах Microsoft Excel для каждого шага и получим следующие результаты:
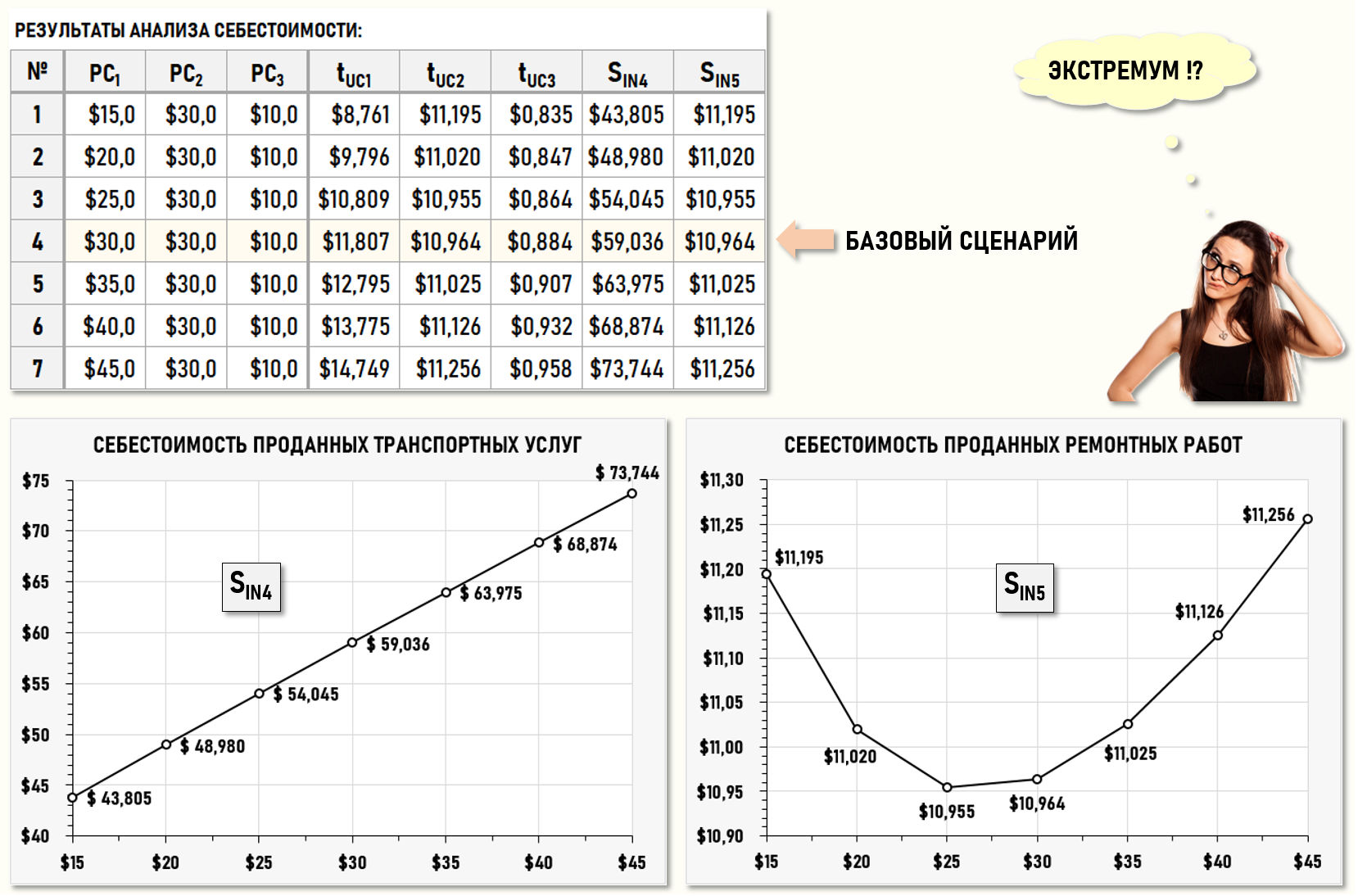
ОБСУЖДЕНИЕ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ (↑)
Поведение целевого показателя SIN4 особых вопросов не вызывает, его значения почти линейно изменяются в след за изменениями значений влияющего фактора pc1.
Поведение же целевого показателя SIN5 можно назвать не совсем ожидаемым. Увеличение значений влияющего фактора pc1 сначала приводит к уменьшению значений целевого показателя SIN5, а затем к их увеличению. Это значит, что в рассмотренном диапазоне значений влияющего фактора pc1 целевой показатель SIN5, во-первых, изменяется нелинейно, а во-вторых, имеет ярко выраженный минимум, что говорит о том, что увеличение стоимости первичных затрат pc1 Цеха 1 (транспорт) может приводить не только к увеличению себестоимости проданных Цехом 2 ремонтных работ, но и к уменьшению(!) их себестоимости.
Откуда у такой маленькой модели предприятия появился такой необычный характер поведения себестоимости? Граф затрат G(5,8) состоит всего из пяти центров затрат, два из которых (CC4 и CC5) являются стоками, которые только получают вторичные затраты и никому их не отдают. Как получилось, что потоки затрат через оставшиеся три центра затрат дали такую интересную реакцию в ответ на изменение значения влияющего фактора pc1?
Причина очевидна – положением об учетной политике предприятия предусмотрено, что распределение стоимости управленческих затрат на выходе центра затрат СС3 производится пропорционально стоимостям первичных затрат, полученных Цехами 1 и 2 в анализируемом периоде. В нашей модели это условие реализуется с помощью формул для вычисления значений исходных коэффициентов:
k3,1=pc1/(pc1+pc2) – доля затрат на управление Цехом 1
k3,2=pc2/(pc1+pc2) – доля затрат на управление Цехом 2
Поскольку стоимость первичных затрат pc2 в нашем примере не изменяется, то эти два исходных коэффициента можно рассматривать как функции от стоимости первичных затрат k3,1(pc1) и k3,2(pc1). Ниже на рисунке представлены диаграммы, характеризующие поведение исходных коэффициентов k3,1 и k3,2 а также всех трех тарифов tUCi при изменении значения влияющего фактора pc1 в диапазоне [15$..45$]:
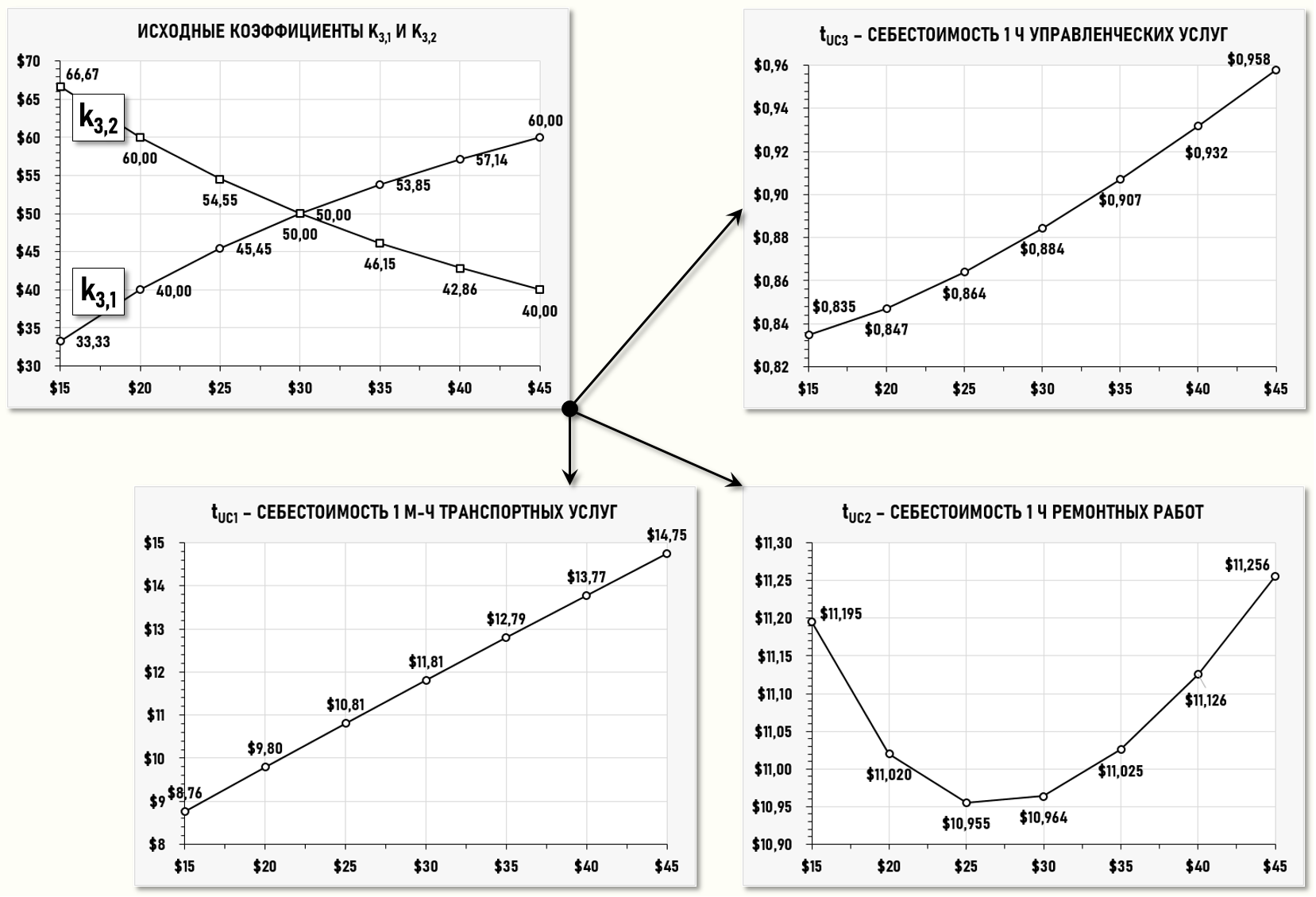
Анализ диаграмм позволяет сделать вывод о том, что нелинейный характер поведения целевого показателя SIN5 – себестоимости проданных ремонтных работ является следствием нелинейного характера поведения пары исходных коэффициентов k3,1 и k3,2, т.е. «неудачно» выбранным способом распределения управленческих затрат между цехами предприятия.
Здесь необходимо сказать несколько слов о выборе методики расчета исходных коэффициентов k3,1 и k3,2. При решении этой задачи необходимо уметь учитывать последствия для хозяйственной деятельности предприятия, т.к. на основе полученной в результате расчетов информации будут приниматься управленческие решения.
Например, если предположить, что административный персонал уделяет одинаковое внимание управлению обоими цехами, то затраты на управление можно просто поделить поровну между Цехом 1 и Цехом 2. В этом случае значения исходных коэффициентов k3,1 и k3,2 всегда будут равны по 50% каждый и не будут зависеть от стоимости первичных затрат цехов предприятия. Результаты анализа себестоимости для этого варианта имеют следующий вид:
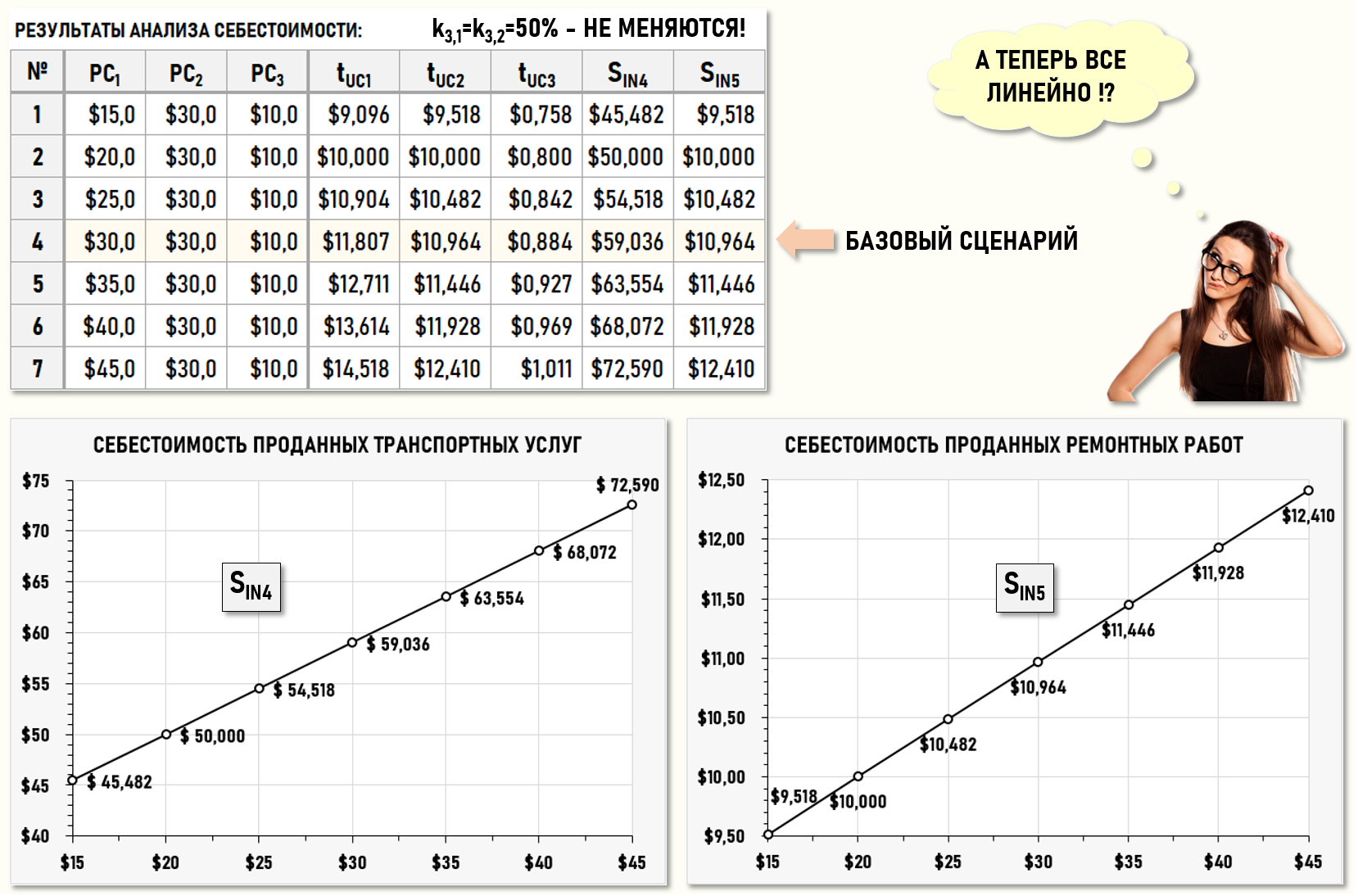
В этом случае наблюдается совсем другое поведение целевых показателей SIN4 и SIN5, как будто речь идет о другом предприятии или о другой производственной программе предприятия. Изменения значений обоих целевых показателей носят исключительно линейный характер, хотя мы всего лишь изменили Положение об учетной политике предприятия, т.е. просто изменили правила расчета двух исходных коэффициентов k3,1 и k3,2, не внося никаких(!) изменений в хозяйственную деятельность предприятия. Если сравнить поведение целевых показателей для обоих вариантов расчета исходных коэффициентов k3,1 и k3,2, то получим следующую картину:
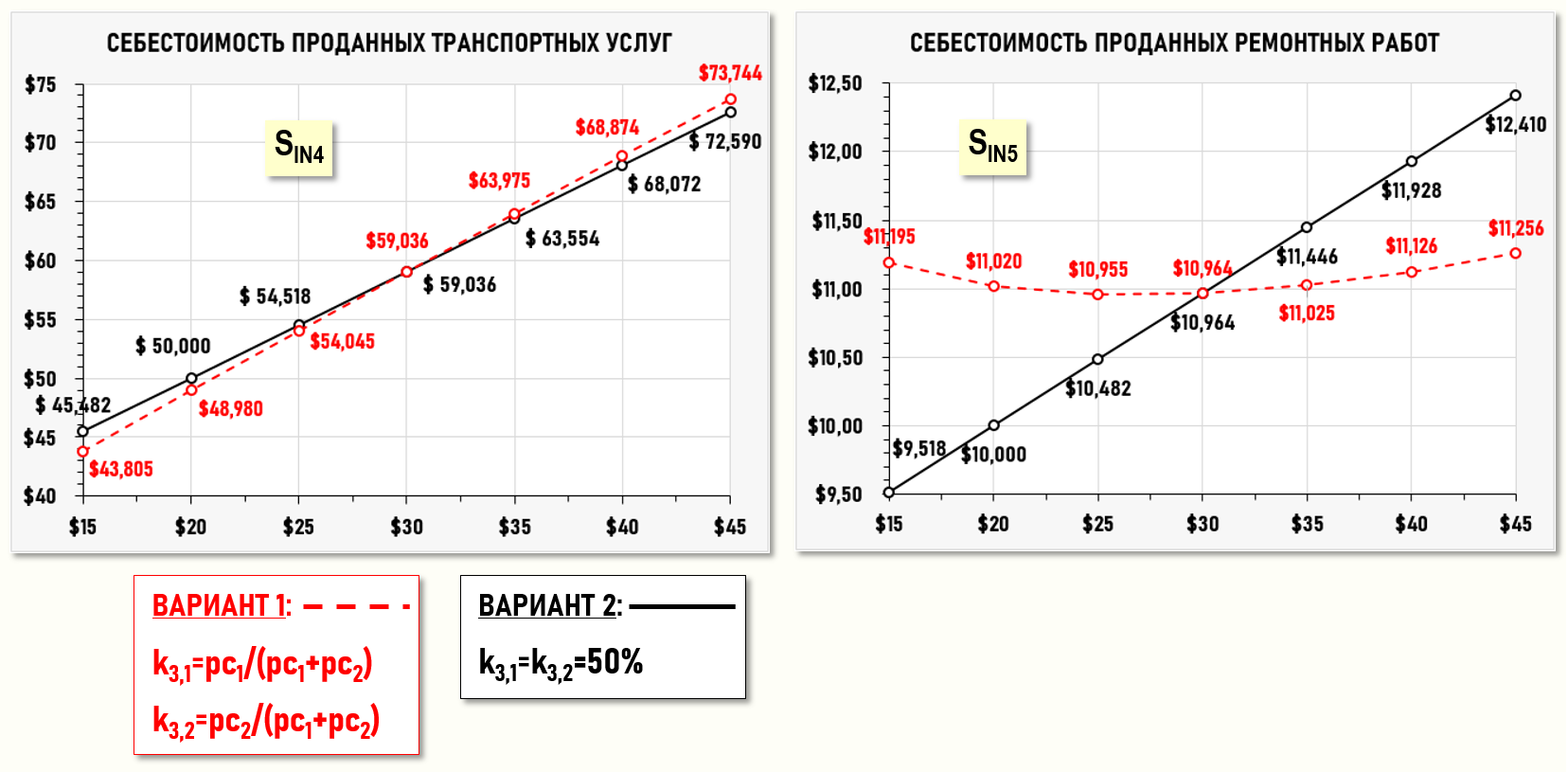
Пунктирной линией на диаграммах показано поведение целевых показателей SIN4 и SIN5 для варианта, когда значения исходных коэффициентов k3,1 и k3,2 изменяются вслед за изменением стоимости первичных затрат pc1.
Сплошной линий показано поведение целевых показателей SIN4 и SIN5 когда значения исходных коэффициентов k3,1 и k3,2 не изменяются вслед за изменением стоимости первичных затрат pc1 и всегда равны 50%.
Если поведение целевого показателя SIN4 для обоих вариантов почти одинаково, то поведение целевого показателя SIN5 имеет существенные отличия для каждого варианта расчета значений исходных коэффициентов k3,1 и k3,2.
Рассмотренный в статье пример достаточно ярко иллюстрирует существующую в настоящее время проблему, заключающуюся в том, что специалисты по расчету себестоимости далеко не всегда понимают, с какими математическими моделями для расчета себестоимости они имеют дело. В результате, для одной и той же производственной программы предприятия в одном и том же периоде можно получить совершенно разные значения себестоимостей в зависимости от субъективных предпочтений конкретных специалистов по расчету себестоимости.
Если в первом варианте специалист по расчету себестоимости при формировании Положения об учетной политике предприятия принимает решение поступать «традиционно», «как все» – и выбирает алгоритм распределения затрат на управление пропорционально стоимостям первичных затрат, то расплатой за это будет «необычное» поведение себестоимости проданных ремонтных работ в процессе анализа себестоимости.
Остается только решить, как относиться к экономическому смыслу полученных результатов? Согласиться с тем, что такое поведение себестоимости проданных ремонтных работ является правильным или все-таки пересмотреть параметры модели, т.е. Положение об учетной политике предприятия?
Для экономистов уже давно не является секретом тот факт, что наиболее экономически корректными являются алгоритмы распределения вторичных затрат «вслед» за натуральными единицами (единицами калькуляции), в которых можно измерить продукцию, работы или услуги на выходе соответствующего центра затрат. В нашем случае объем работы управленческого персонала можно, например, измерить в человеко-часах. Для этого, правда, необходимо вести раздельный учет потраченного управленческим персоналом времени для управления Цехом 1 и Цехом 2. Также необходимо будет уметь прогнозировать распределение этого времени при различных сценариях производственных программ предприятия. Но только в этом случае можно будет с достаточной степенью уверенности говорить не только о математической, но и об экономической корректности нашей модели. Причем, поведение модели в этом случае также может оказаться нелинейным, но это будет уже реальная нелинейность, а не выдуманная учетным сотрудником предприятия, как в рассмотренном выше примере.

