Расчет себестоимости (СЛАУ). Затраты в НЗП
Автор: Александр Поляков
В данной статье будет рассмотрена процедура расчета себестоимости (закрытия затрат периода) для случая, когда на предприятии присутствуют затраты в незавершенном производстве (НЗП) на начало и на конец отчетного периода. Расчет себестоимости (решение СЛАУ) будет произведен с помощью типового функционала Microsoft Excel.
Изучать эту процедуру будем на примере небольшого производственного предприятия, рекомендуется скачать таблицы Microsoft Excel для рассматриваемого примера и работать с ними в процессе изучения материала статьи.
Формирование СЛАУ в матричной форме
Решение СЛАУ (нахождение тарифов)
«Неправильные» затраты в НЗП. Отрицательные стоимости
УСЛОВИЯ ЗАДАЧИ (↑)
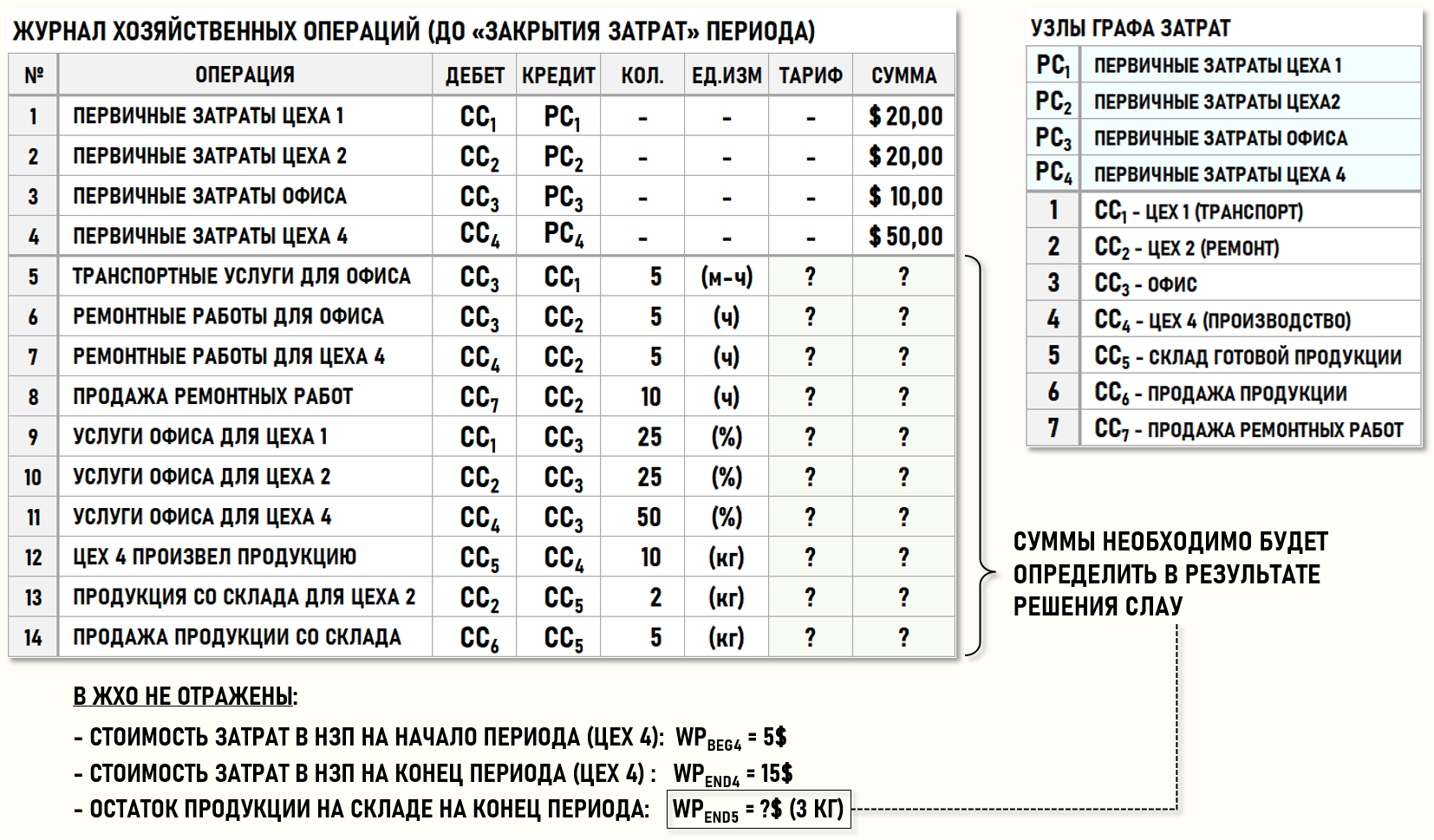
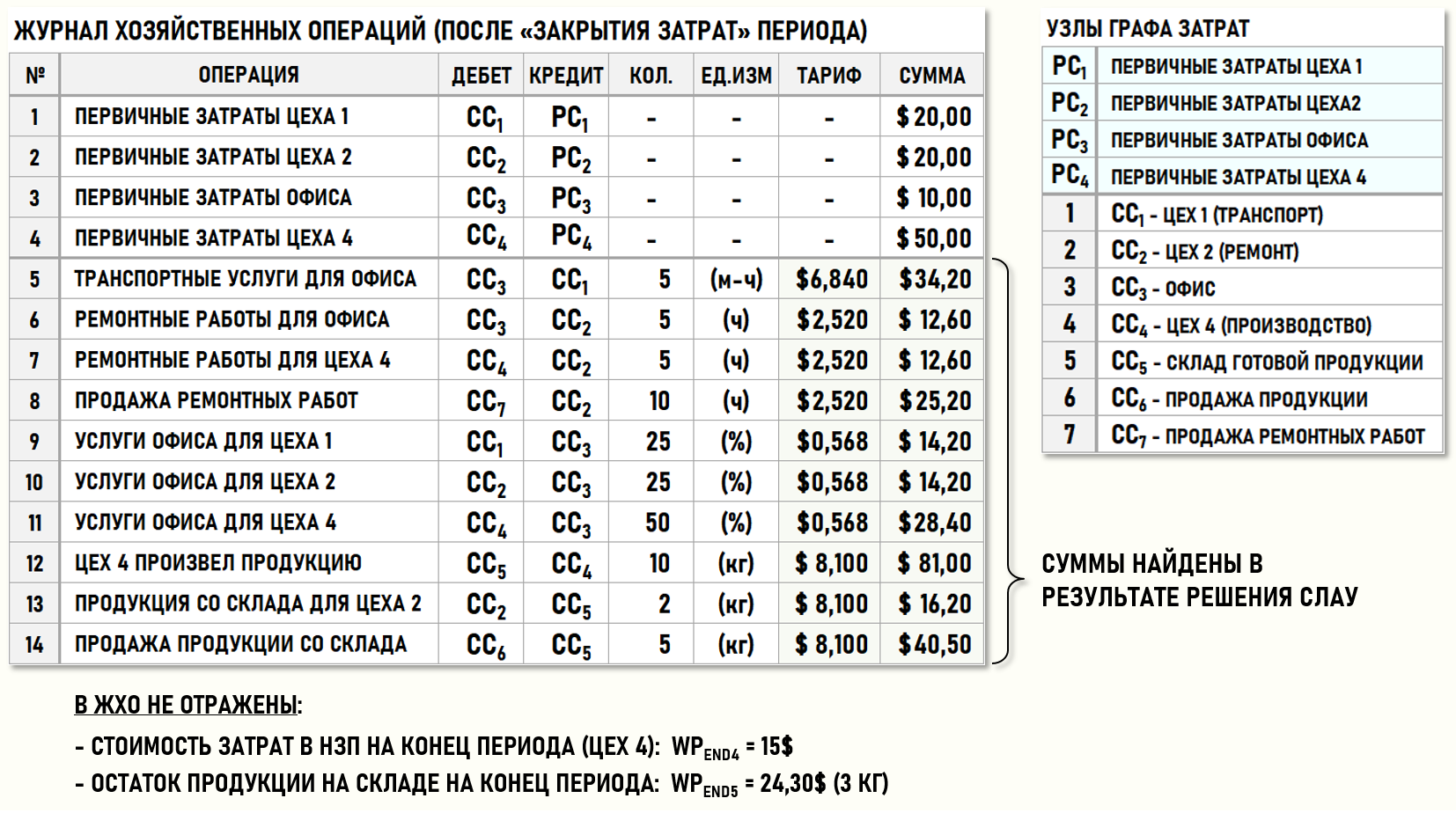
Предприятие осуществляет два вида деятельности – производит и продает продукцию, а также выполняет (продает) для сторонних контрагентов ремонтные работы. Ниже на рисунке представлен журнал хозяйственных операций (ЖХО) предприятия за отчетный период:.
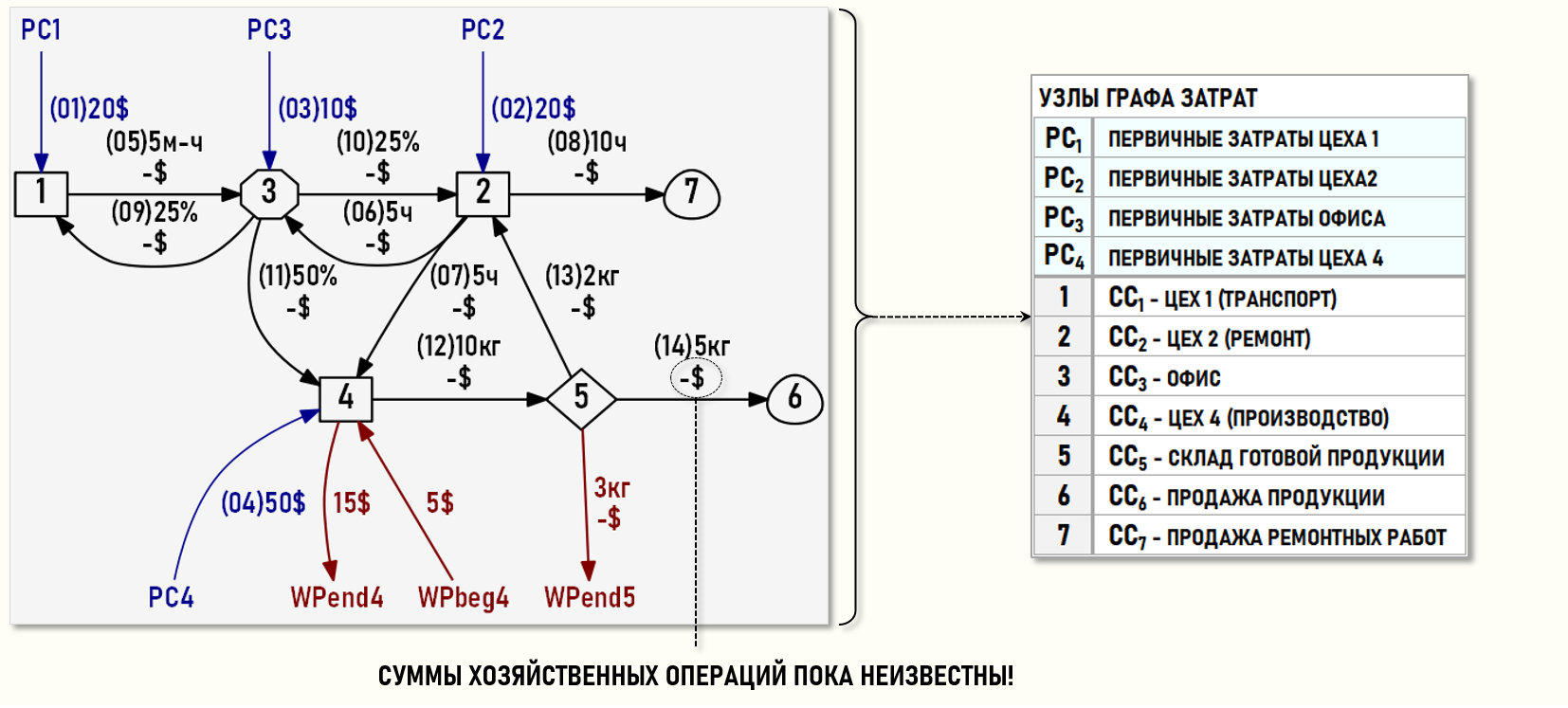
Также представим множество хозяйственных операций отчетного периода в геометрической форме, т.е. в виде нарисованного Графа затрат, дуги которого идентифицируются с помощью номеров хозяйственных операций из ЖХО (в скобках), весами дуг выступают количества единиц калькуляции и суммы хозяйственных операций.
Цех 1 (СС1) оказал транспортные услуги Офису (СС3) в количестве 5-ти машино-часов.
Цех 2 (СС2) выполнил ремонтные работы для Офиса (СС3) и Цеха 4 (СС4) в количестве 5-ти часов каждому, а также для сторонних контрагентов в количестве 10-ти часов (продал ремонтные работы). Себестоимость проданных ремонтных работ формируется на входе центра затрат СС7.
Цех 4 (СС4) произвел 10 килограммов продукции и поместил ее на склад предприятия (СС5). Часть продукции со склада (5кг) была продана покупателям, часть продукции (2кг) в этом же периоде была использована Цехом 2 (СС2) для производства ремонтных работ. В конце периода на складе осталось 3кг продукции, произведенной в отчетном периоде. Себестоимость проданной продукции формируется на входе центра затрат СС6.
На начало отчетного периода в Цехе 4 (СС4) присутствовала продукция, не прошедшие все стадии технологического процесса, т.е. присутствовали затраты в НЗП стоимостью 5$. На конец отчетного периода в Цехе 4 (СС4) остались затраты в НЗП стоимостью 15$.
Управление деятельностью предприятия производится административным персоналом в Офисе (СС3). Распределение стоимости управленческих затрат Офиса (СС3) производится в следующих пропорциях – по 25% получают Цех 1 (СС1) и Цех 2 (СС2), а оставшиеся 50% приходятся на долю Цеха 4 (СС4). В данном случае рассчитываются полные себестоимости проданных продукции и ремонтных работ, поскольку в них включаются стоимости затрат на управление предприятием.
Пока не будет выполнена процедура закрытия затрат периода, только четыре хозяйственные операции (с 1-ой по 4-ую) будут иметь не 0-вые стоимости, поскольку стоимости первичных затрат всегда известны до начала процедуры закрытия затрат периода.
Остальные хозяйственные операции (с 5-ой по 14-ю) характеризуются пока только количествами единиц калькуляции. Стоимости хозяйственных операций, а также стоимость оставшейся на складе продукции (3кг) будут определены по результатам выполнения процедуры расчета себестоимости – закрытия затрат периода.
ФОРМИРОВАНИЕ СЛАУ В МАТРИЧНОЙ ФОРМЕ (↑)
Общий вид СЛАУ в матричной форме для нашей задачи имеет следующий вид:
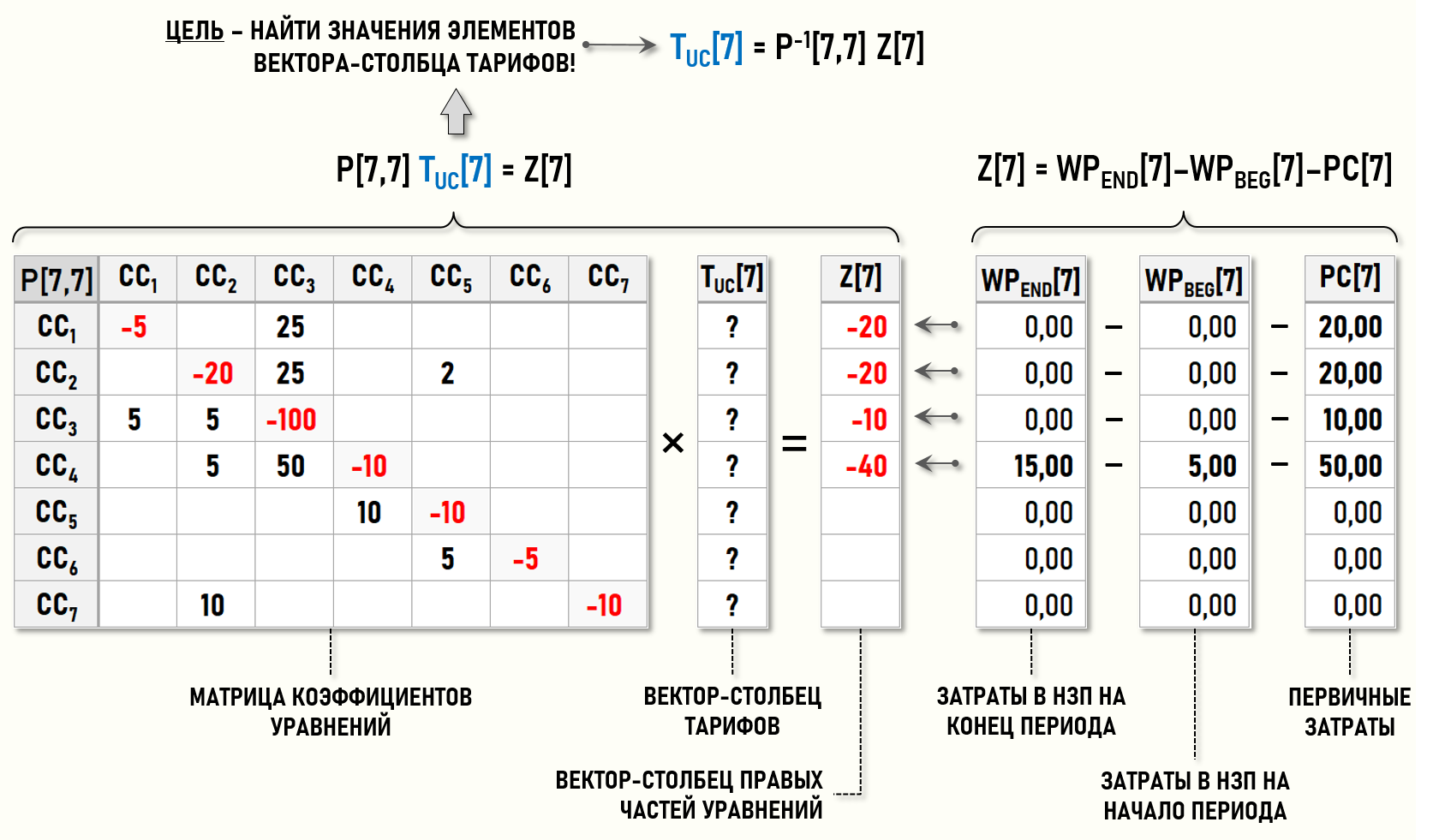
P[7,7] TUC[7]=Z[7]
где:
P[7,7] – матрица коэффициентов уравнений
TUC[7] – вектор-столбец тарифов
Z[7] – вектор-столбец правых частей уравнений
Целью решения СЛАУ является нахождение вектора-столбца тарифов ТUC[7]:
TUC[7]=P-1[7,7] Z[7]
где:
P-1[7,7] – обратная матрица коэффициентов уравнений
В статье будет использован вариант формирования входящих в СЛАУ матриц, основанный на понижении размерности задачи за счет исключения из СЛАУ уравнений для центров затрат CC6 и CC7, которые являются стоками и используются для формирования себестоимости проданной продукции и проданных ремонтных работ.
Матричная форма СЛАУ для нашей задачи имеет следующий вид:
Матрица коэффициентов уравнений P[7,7] и вектор-столбец правых частей уравнений Z[7] формируются на основе учетных данных из ЖХО. Ячейки на главной диагонали матрицы P[7,7] для центров затрат CC6 и CC7 также заполнены значениями коэффициентов уравнений, хотя в ЖХО отсутствуют хозяйственные операции с этими данными. С формальной точки зрения количества проданной продукции (5кг) и проданных ремонтных работ (10ч) формируют затраты в НЗП на конец периода для этих центров затрат.
Напомним, что общий термин «затраты в НЗП» используется в теории Графов затрат для обозначения затрат, остающихся в центрах затрат любого класса на начало или на конец периода. С этой точки зрения стоки CC6 и CC7 также могут иметь затраты в НЗП, в данном случае затраты в НЗП на конец периода для центра затрат CC6 характеризуют количество проданной продукции (5кг), а для центра затрат CC7 – количество проданных ремонтных работ (10ч).
Для решения полученной СЛАУ надо найти обратную матрицу коэффициентов уравнений P-1[7,7] и умножить ее на вектор-столбец Z[7], в результате будет найден искомый вектор-столбец тарифов TUC[7]. Умножив далее полученные тарифы на количества единиц калькуляции можно будет найти стоимости хозяйственных операций с 5-ой по 14-ю.
Рассмотрим подробнее процедуру решения СЛАУ с помощью типового функционала Microsoft Excel.
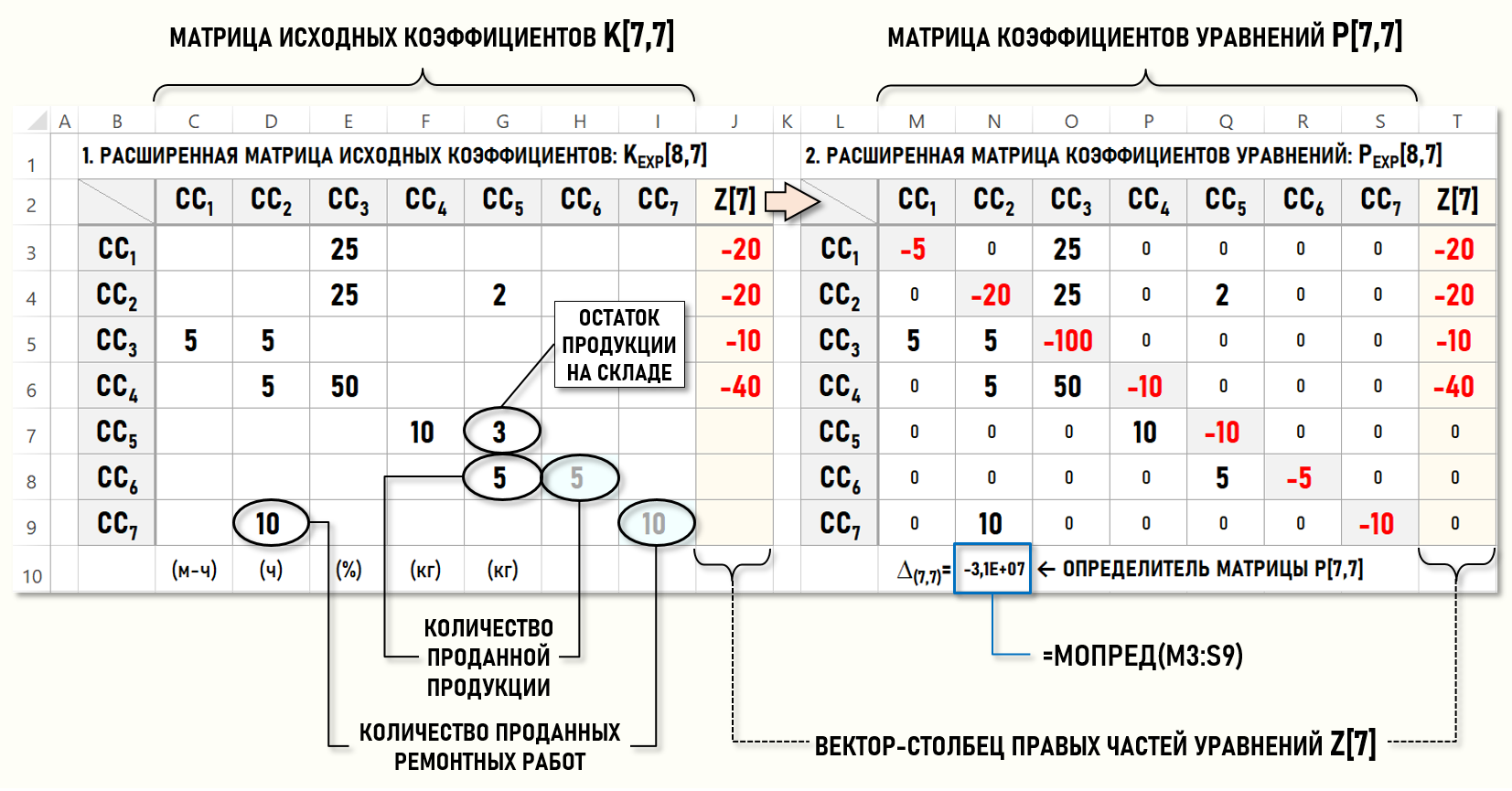
Для начала представим полученную СЛАУ в более удобном для практической работы виде – с помощью расширенной матрицы коэффициентов уравнений PEXP[8,7], состоящей из квадратной матрицы коэффициентов уравнений P[7,7] и присоединенного к ней справа вектора-столбца правых частей уравнений Z[7].
Работа с таблицами Microsoft Excel предполагает некоторые особенности – все пустые ячейки матрицы PEXP[8,7] необходимо заполнить 0-ми, это связано с технологическими особенностями вычисления некоторых функций.
На рисунке также показана и расширенная матрица исходных коэффициентов KEXP[8,7], которая не присутствует в явном виде в СЛАУ, но очень удобна для практической работы, т.к. позволяет в наглядной и компактной форме представить всю необходимую для распределения вторичных затрат информацию. Эту матрицу можно рассматривать в качестве «интерфейса» модели для расчета себестоимости.
Например, в нашем случае в столбце для Склада (CC5) в матрице KEXP[8,7] наглядно видно не только куда и сколько в отчетном периоде передавалось продукции, но и сколько продукции осталось на Складе (CC5) на конец периода. В аналогичном столбце матрицы PEXP[8,7] эта информация представлена гораздо менее наглядным образом.
Как известно, формирование расширенной матрицы коэффициентов уравнений PEXP[8,7] из расширенной матрицы исходных коэффициентов KEXP[8,7] происходит единственным образом и фактически представляет собой чисто «техническую» задачу.
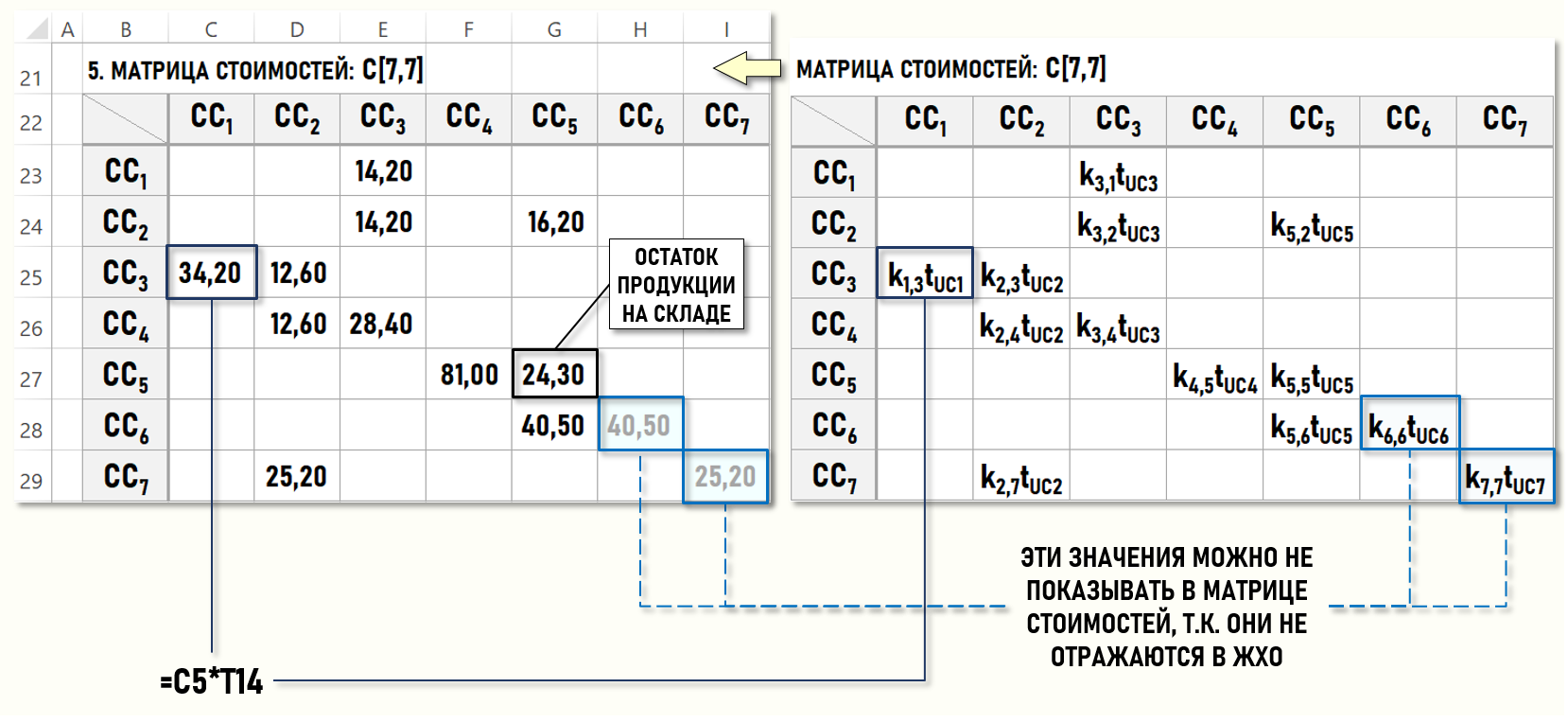
На практике, при использовании варианта расчета себестоимости, основанного на уменьшении размерности СЛАУ, часто не заполняют диагональные элементы матриц для стоков, в которых формируются расходы предприятия, поскольку, с одной стороны, далее в расчетах они не учитываются, а с другой стороны, уменьшают наглядность матриц. Например, выше на рисунке количества проданных продукции и ремонтных работ показаны два раза, один раз в столбцах для CC2 и CC5, и второй раз – в столбцах для CC6 и CC7, что явно избыточно для пользователя модели.
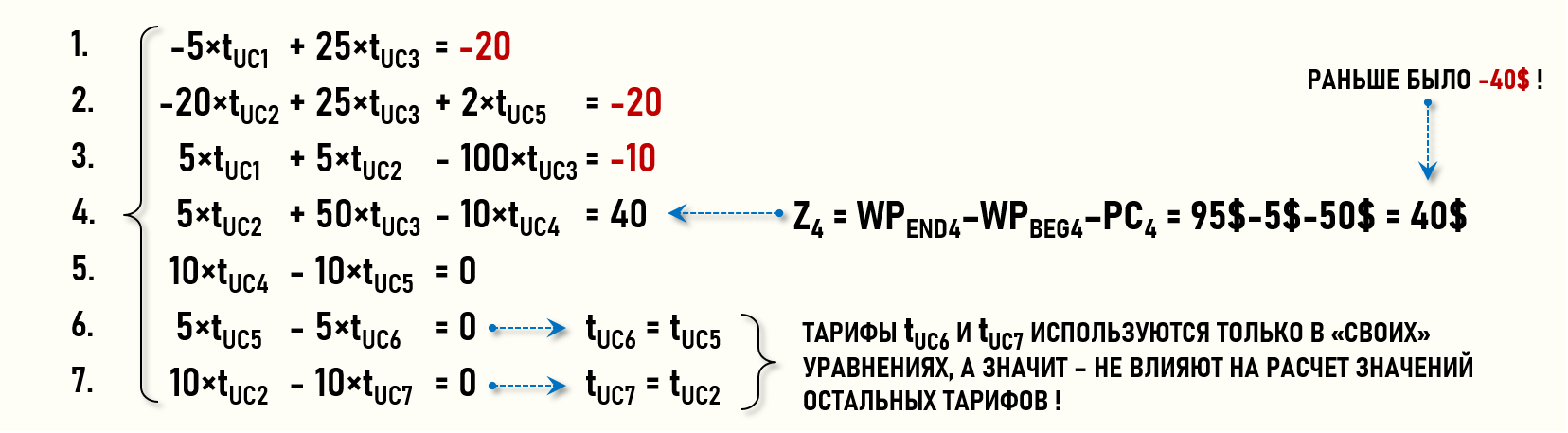
Если представить СЛАУ в «обычной» форме, то легко увидеть, что уравнения 6 и 7 фактически не нужны, т.к. тарифы tUC6 и tUC7 используются только в «своих» уравнениях, а значит – не влияют на расчет значений остальных тарифов.
Это позволяет уменьшить число уравнений в СЛАУ с 7-ми до 5-ти. Исключив из рассмотрения столбцы и строки для стоков CC6 и CC7, преобразуем матрицу РEXP[8,7] в матрицу меньшей размерности – РEXP[6,5]:
Вычисленное в ячейке C19 значение определителя матрицы Р[5,5] отлично от 0-ля:
∆(5,5)=МОПРЕД(C14:G18)=-6,3×105≠0
Можно продолжить поиск единственного решения СЛАУ.
РЕШЕНИЕ СЛАУ (НАХОЖДЕНИЕ ТАРИФОВ) (↑)
После уменьшения размерности задачи формула для нахождения значений тарифов примет следующий вид:
TUC[5]=P-1[5,5] Z[5]
Для нахождения обратной матрицы коэффициентов уравнений Р-1[5,5] воспользуемся функцией Microsoft Excel МОБР(), которая вводится как формула массива, предполагающая выполнение следующих действий:
- в ячейку M14 вводится формула МОБР(C14:G18)
- выделяется курсором область ячеек (M14:Q18)
- не отменяя выделения ячеек области нажимается клавиша F2
- одновременно нажимается комбинация клавиш Shift+Ctrl+Enter
В результате в области ячеек (M14:Q18) будет сформирована обратная матрица коэффициентов уравнений P-1[5,5].
После этого выполняется последний шаг процедуры решения СЛАУ – матрица Р-1[5,5] умножается на вектор-столбец Z[5] и определяются значения элементов вектора-столбца тарифов TUC[5].
Перемножение матриц производится функцией Microsoft Excel МУМНОЖ(масив1,массив2). При выборе очередности массивов для перемножения необходимо, чтобы количество столбцов в массив1 было таким же, как количество строк в массив2:
МУМНОЖ(M14:Q18;R14:R18)
где:
массив1=(M14:Q18) – обратная матрица коэффициентов уравнений Р-1[5,5]
массив2=(R14:R18) – вектор-столбец правых частей уравнений Z[5]
Данная функция вводится как формула массива:
- в ячейку T14 вводится формула МУМНОЖ(M14:Q18;R14:R18)
- выделяется курсором область ячеек (T14:T18)
- не отменяя выделения ячеек области нажимается клавиша F2
- одновременно нажимается комбинация клавиш Shift+Ctrl+Enter
В результате в области ячеек (T14:T18) сформируются искомые значения тарифов, т.е. будет найдено решение СЛАУ.
МАТРИЦА СТОИМОСТЕЙ (↑)
Теперь осталось определить значения элементов матрицы стоимостей C[7,7], для чего надо умножить значения элементов матрицы исходных коэффициентов К[7,7] на соответствующие значения тарифов из вектора-столбца ТUC[5].
В ячейках матрицы стоимостей C[7,7] содержатся все стоимости вторичных затрат, т.е. стоимости хозяйственных операций с 5-ой по 14-ю, которые теперь можно записать в ЖХО, как и значения тарифов из вектора-столбца TUC[5]:
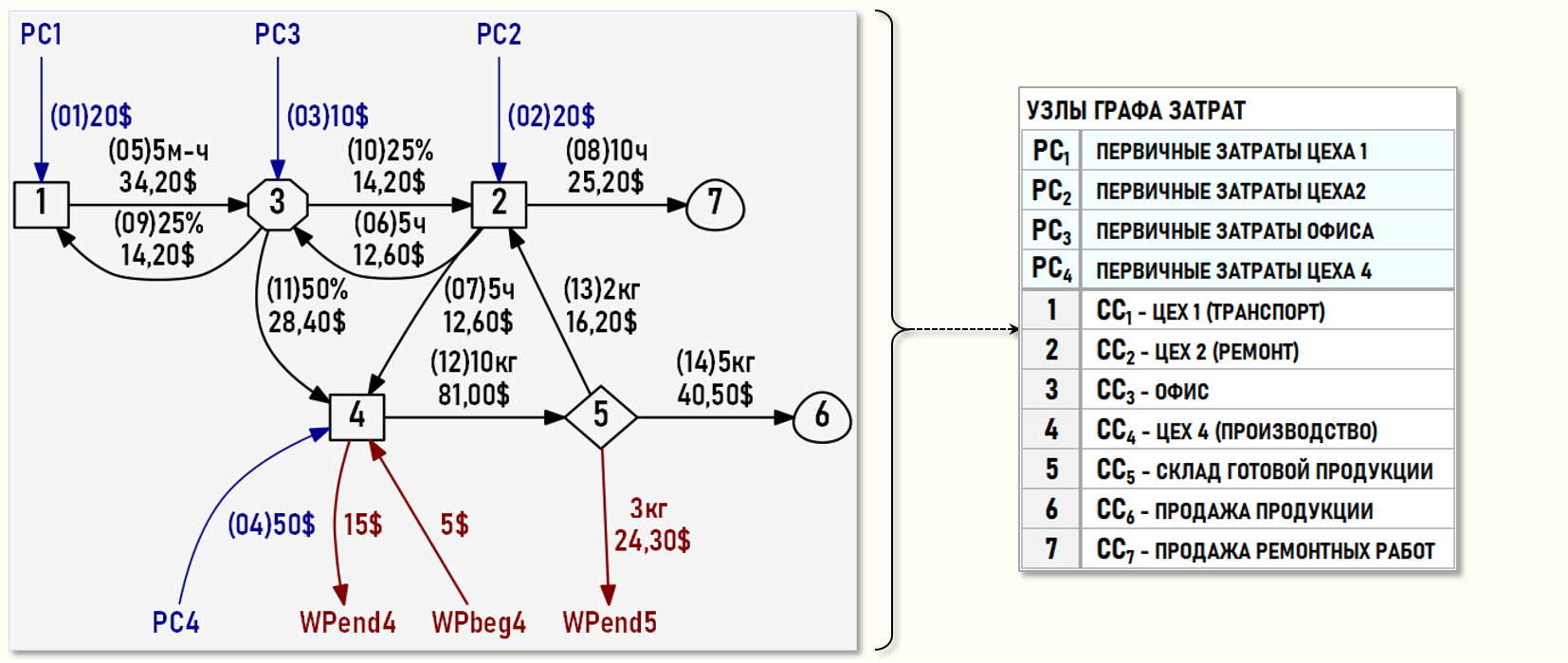
Также представим множество хозяйственных операций в виде нарисованного Графа затрат, весами дуг которого являются номера операций из ЖХО (в скобках), количества единиц калькуляции и суммы операций.
ПРОВЕРКА РЕШЕНИЯ СЛАУ (↑)
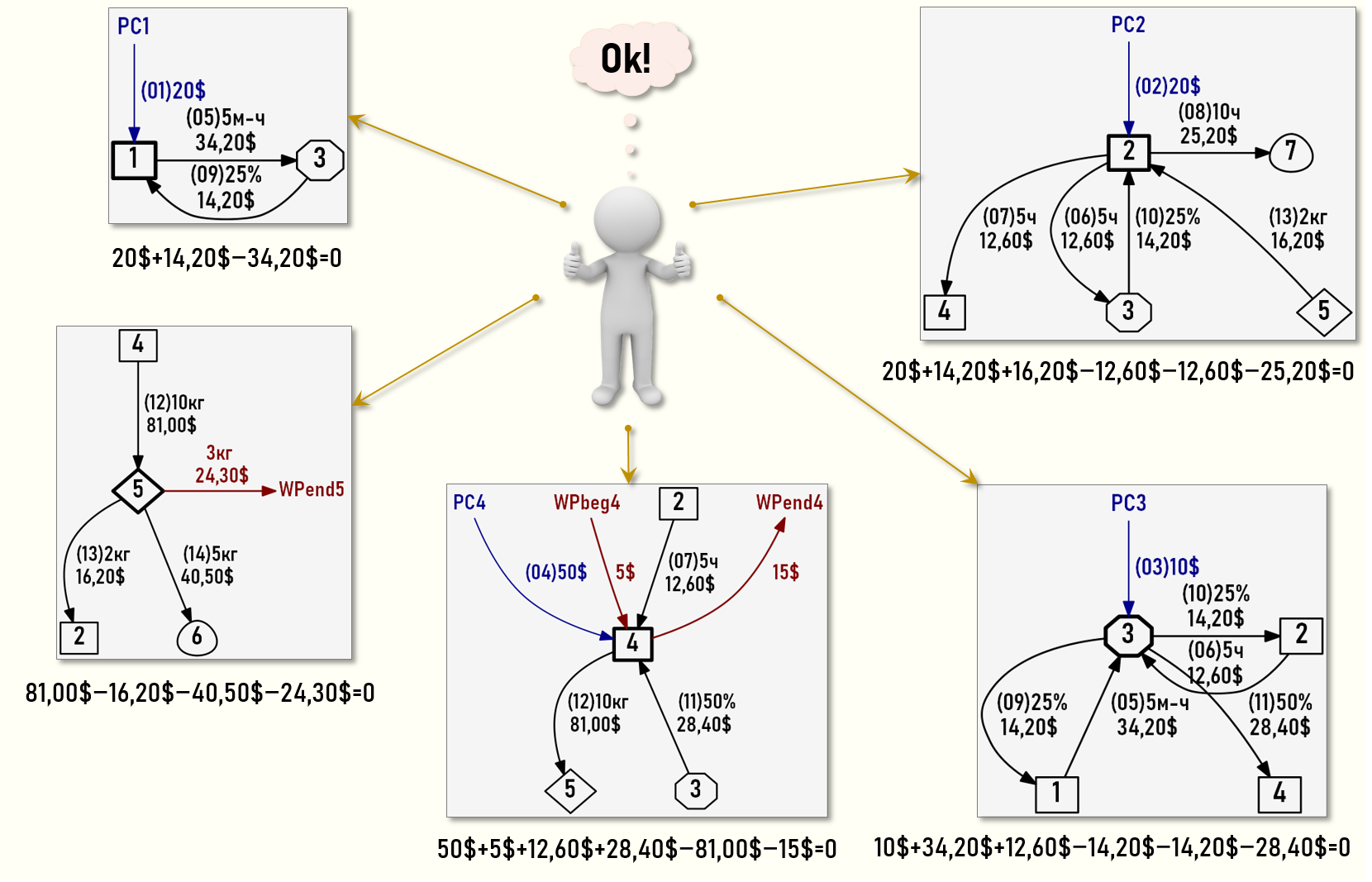
Проверим, выполняются ли уравнения баланса затрат для всех центров затрат нашего Графа затрат?
В «обычном» виде СЛАУ будет выглядеть следующим образом:
Представим также потоки затрат для каждого центра затрат в геометрической форме:
На рисунке видно, что все уравнения баланса затрат выполняются, т.е. решение СЛАУ, а значит и стоимости всех хозяйственных операций найдены правильно!
«НЕПРАВИЛЬНЫЕ» ЗАТРАТЫ В НЗП. ОТРИЦАТЕЛЬНЫЕ СТОИМОСТИ (↑)
В рассмотренном примере присутствуют стоимости затрат в НЗП у двух центров затрат, относящихся к разным классам и имеющих свои особенности составления уравнений баланса затрат:
- затраты в НЗП в Цехе 4 (CC4) на начало и на конец отчетного периода
- затраты в НЗП – оставшаяся в конце отчетного периода продукция на Складе (CC5)
Для остатка продукции на Складе (CC5) проблема затрат в НЗП на конец периода решается просто, в этом случае количество продукции (3кг) отражается на главной диагонали матриц K[7,7] и P[7,7] для центра затрат CC5.
С затратами в НЗП для Цеха 4 (CC4) ситуация несколько сложнее, поскольку в данном случае стоимость затрат в НЗП принимает участие в формировании правой части уравнения баланса затрат для центра затрат CC4.
Это довольно «неприятная» особенность модели для расчета себестоимости, поскольку стоимости затрат в НЗП на начало и на конец периода должны быть известны до начала процедуры закрытия затрат периода. И если стоимость затрат в НЗП на начало периода должна быть известна по результатам расчета себестоимости предыдущего периода, то стоимость затрат в НЗП на конец периода необходимо каким-то образом определить. Например, это можно сделать по результатам инвентаризации остатков незавершенной производством продукции и ее оценки каким-либо способом, т.е. фактически – достаточно субъективно.
Понятно, что в этом случае правая часть уравнения баланса затрат становится «чувствительной» к предпочтениям учетного специалиста в выборе способа оценки затрат в НЗП и может приводить к ошибкам при расчете себестоимости. Рассмотрим, как это может произойти.
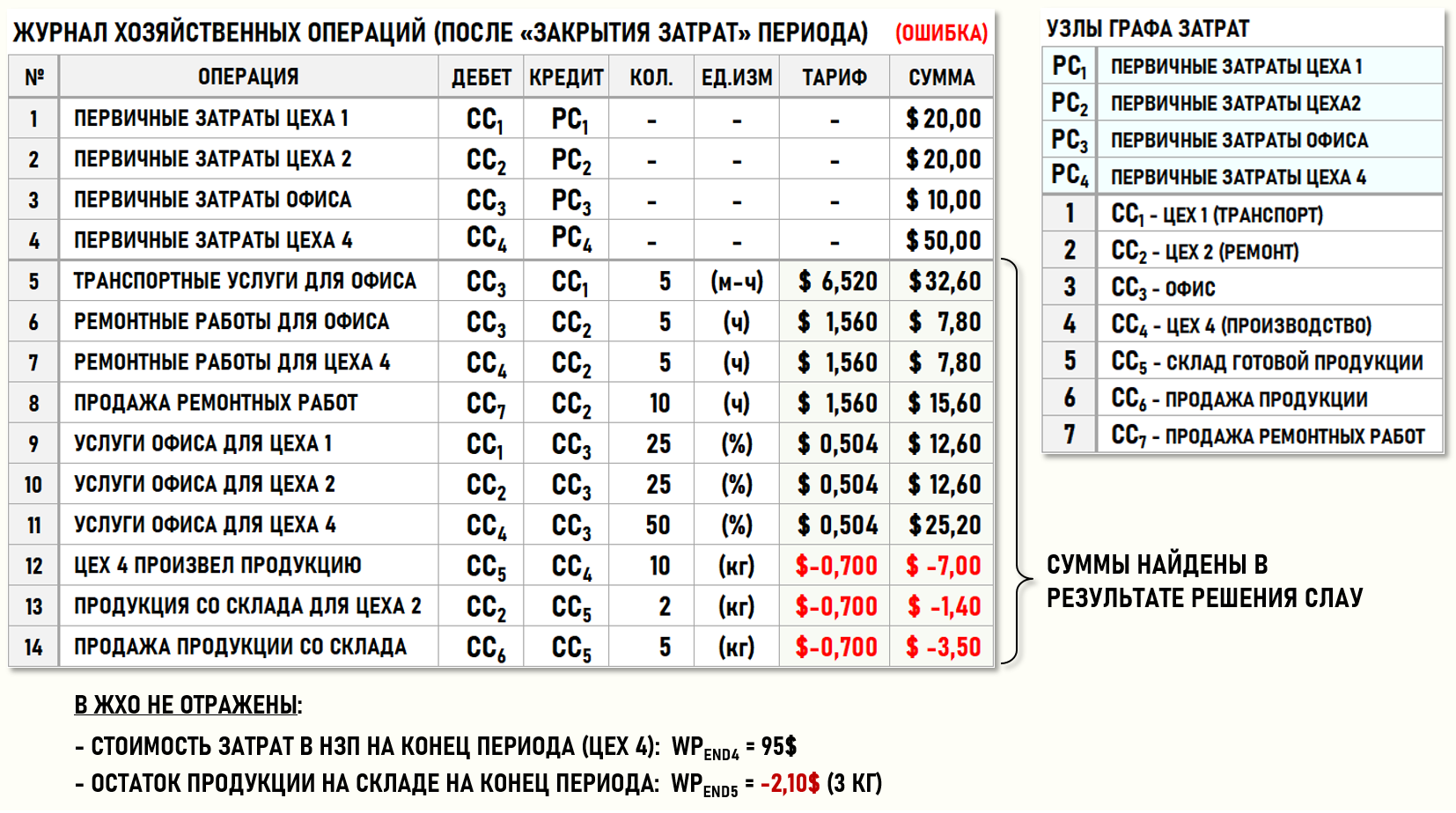
Предположим, что в рассмотренной выше задаче учетный специалист после проведения инвентаризации незавершенного производства в Цехе 4 (CC4) оценил стоимость затрат в НЗП на конец периода как:
WPEND4=95$ (а не 15$ – как ранее)
В этом случае изменится значение правой части уравнения баланса затрат для Цеха 4 (CC4), и СЛАУ примет следующий вид:
Мы не будем подробно рассматривать всю процедуру решения СЛАУ (можно посмотреть ее в таблицах), а сразу покажем полученный результат:
Как видно на рисунке, на выходе центров затрат CC4 и CC5 получились отрицательные значения тарифов, т.е. себестоимость произведенной и помещенной на склад продукции оказалась отрицательной! Это можно увидеть также в матрице стоимостей C[7,7]:
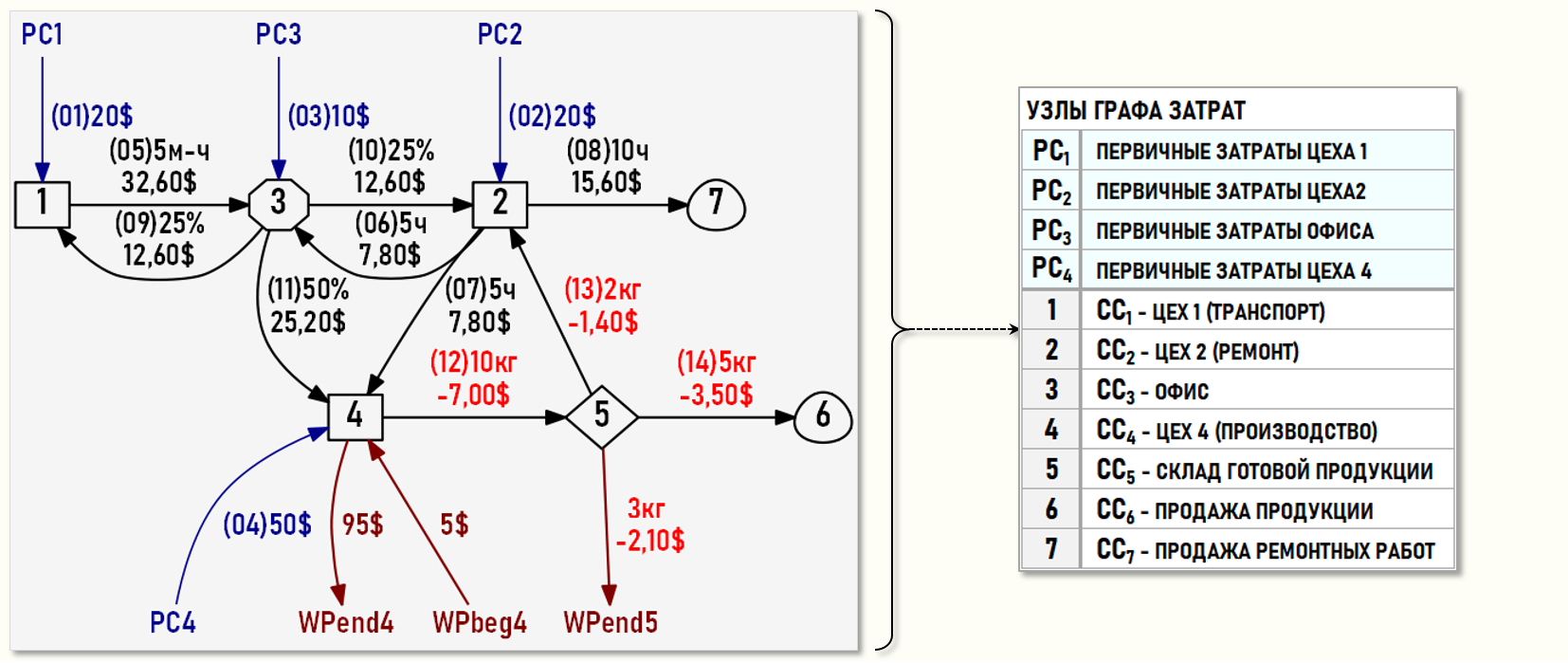
а также в ЖХО и на «нарисованном» Графе затрат:
Что означают полученные результаты решения СЛАУ с математической точки зрения и с точки зрения экономического смысла? Сначала проверим, выполняются ли уравнения баланса затрат во всех центрах затрат модели:
Как видно на рисунке, все уравнения баланса затрат выполняются, т.е. решение СЛАУ с математической точки зрения корректно.
Что же касается экономического смысла полученных результатов, то здесь имеет место очевидная ошибка учетного специалиста при оценке стоимости затрат в НЗП на конец периода WPEND4=95$ для Цеха 4 (CC4). В данном сценарии хозяйственной деятельности предприятия ни при каких условиях получить такую стоимость затрат в НЗП невозможно.
Таким образом, как уже говорилось выше, необходимость учитывать стоимость затрат в НЗП при формировании правых частей уравнений баланса затрат является «неприятной» особенностью модели для расчета себестоимости. Избежать данной ситуации можно только в случае построения существенно более подробной модели предприятия для расчета себестоимости.