Расчет стоимости встречных затрат
Автор: Александр Поляков
В статье Как появляются встречные затраты мы выяснили, что наличие встречных затрат в модели предприятия для расчета себестоимости не представляет собой какое-то исключительное явление и, более того, встречные затраты могут присутствовать в модели для расчета себестоимости у любого предприятия независимо от отраслевых особенностей его хозяйственной деятельности. Также мы выяснили, что нет никакой необходимости вести какую-либо «борьбу» со встречными затратами, поскольку это свидетельствует просто о непонимании пользователями особенностей работы модели для расчета себестоимости.
В статье Способы распределения затрат – прямой, пошаговый и с помощью СЛАУ было показано, что в настоящее время все способы расчета себестоимости основаны на математической модели, представляющей собой систему уравнений баланса затрат для каждого центра затрат (или счета учета затрат), т.е. систему линейных алгебраических уравнений (СЛАУ). Все так называемые «разные» способы расчета себестоимости являются разновидностями способа расчета себестоимости с помощью решения СЛАУ, для которого не существует никакой «проблемы» встречных затрат.
Собственно, на этом данную статью можно было бы и завершить, но для иллюстрации вышесказанного рассмотрим небольшой пример расчета себестоимости для случая, когда в модели хозяйственной деятельности предприятия присутствуют встречные потоки затрат.
Как найти встречные потоки затрат?
Решение СЛАУ (нахождение тарифов)
УСЛОВИЯ ЗАДАЧИ (наверх)
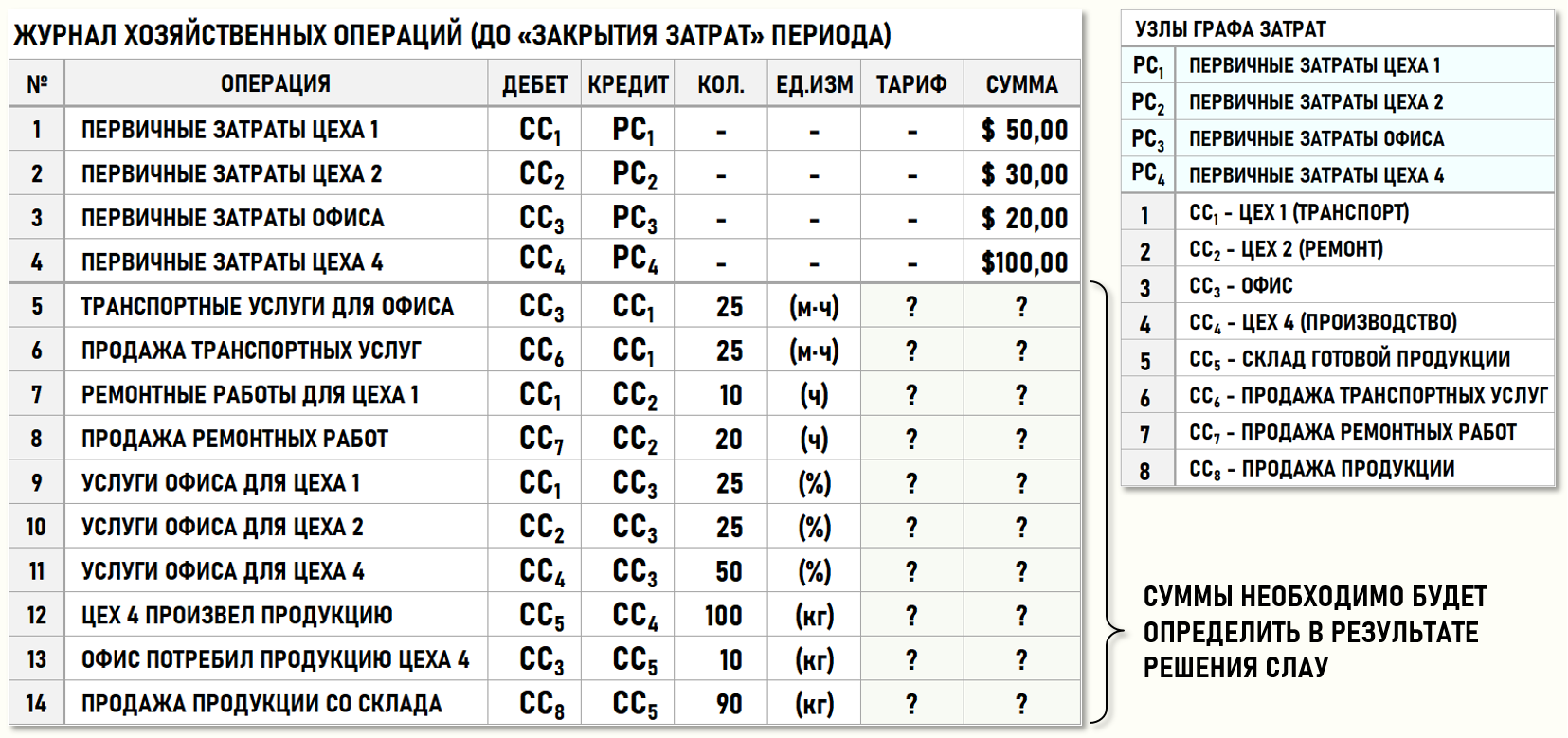
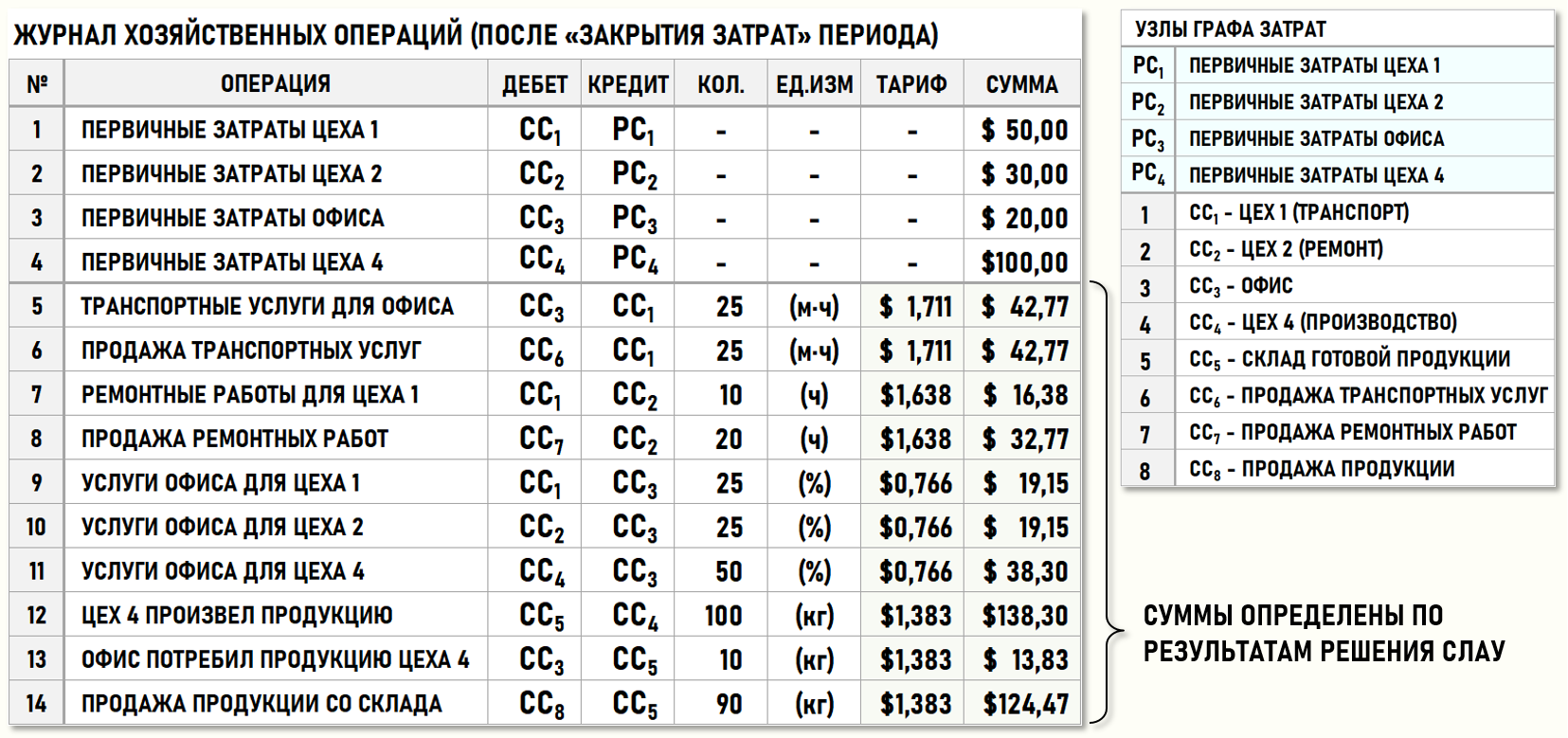
Рассмотрим предприятие, хозяйственная деятельность которого в отчетном периоде представлена ниже на рисунке с помощью журнала хозяйственных операций (ЖХО):
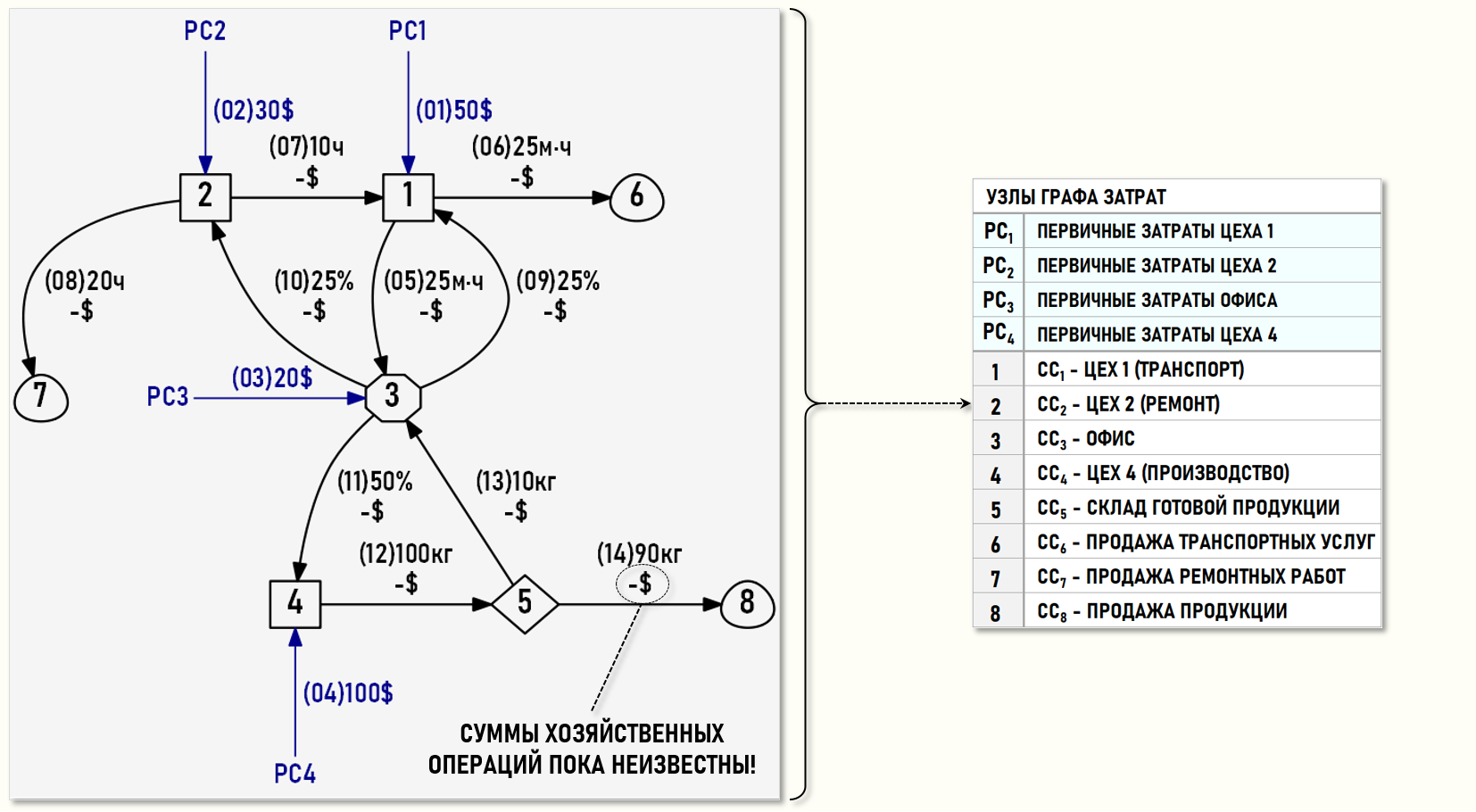
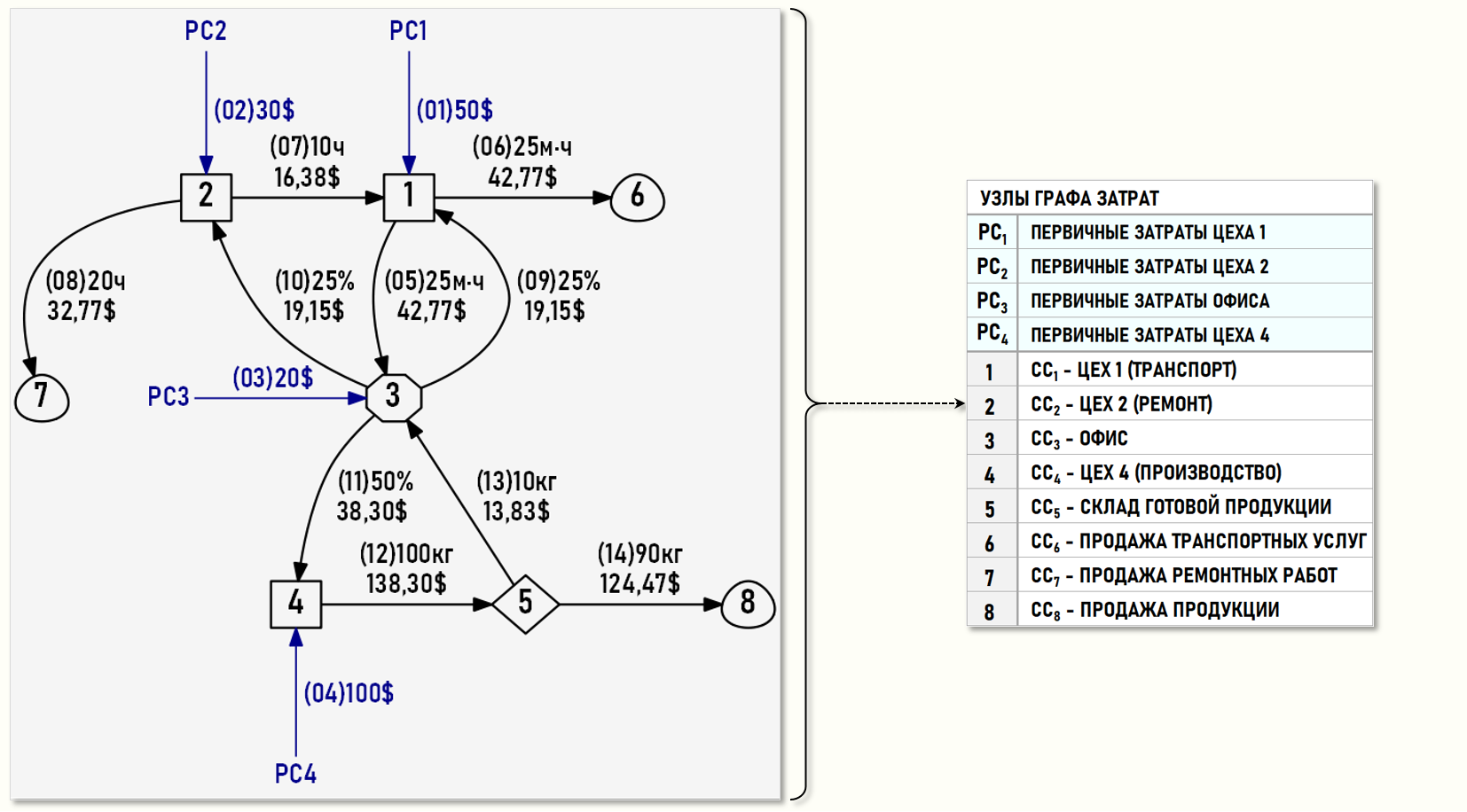
Для наглядности также представим множество хозяйственных операций отчетного периода в геометрической форме – в виде нарисованного Графа затрат, дуги которого идентифицируются с помощью номеров хозяйственных операций из ЖХО (в скобках), весами дуг выступают количества единиц калькуляции и суммы хозяйственных операций.
Предприятие состоит из трех цехов и офиса, в котором сосредоточен административный персонал предприятия.
Цех 1 (СС1) оказывает транспортные услуги Офису (СС3) и сторонним контрагентам, т.е. продает транспортные услуги. Количество этих услуг измеряется в машино-часах (м·ч). Себестоимость проданных транспортных услуг формируется на входе финишного центра затрат СС6.
Цех 2 (СС2) выполняет ремонтные работы для Цеха 1 (СС1) и продает ремонтные работы покупателям. Объемы этих работ измеряются в часах (ч). Себестоимость проданных ремонтных работ формируется на входе финишного центра затрат СС7.
Цех 4 (СС4) производит продукцию (писчую бумагу) и помещает ее на Склад (СС5) предприятия, с которого часть продукции поступает в этом же периоде в Офис (СС3), где используется для составления различных документов, а оставшаяся часть продукции продается покупателям. Количество продукции измеряется в килограммах (кг). Себестоимость проданной продукции формируется на входе финишного центра затрат СС8.
Офис (СС3) оказывает услуги управления всем трем цехам предприятия. Стоимость услуг управления Офиса (СС3) распределяется между Цехом 1 (25%), Цехом 2 (25%) и Цехом 4 (50%).
Пока не будет выполнена процедура закрытия затрат периода, только четыре хозяйственные операции (с 1-ой по 4-ую) будут иметь не 0-вые стоимости. Остальные хозяйственные операции (с 5-ой по 14-ю) характеризуются пока только количествами единиц калькуляции. Стоимости этих хозяйственных операций будут определены по результатам выполнения процедуры расчета себестоимости – закрытия затрат периода.
КАК НАЙТИ ВСТРЕЧНЫЕ ПОТОКИ ЗАТРАТ? (наверх)
Напомним критерий, позволяющий определить наличие в Графе затрат встречных потоков затрат:
ЕСЛИ: два центра затрат CCi и CCj достижимы друг из друга, т.е. существует орцепь из CCi в CCj и орцепь из CCj в CCi
ТО: эти центры затрат связаны встречными потоками вторичных затрат
Посмотрим, как можно использовать данное правило для нашего Графа затрат:
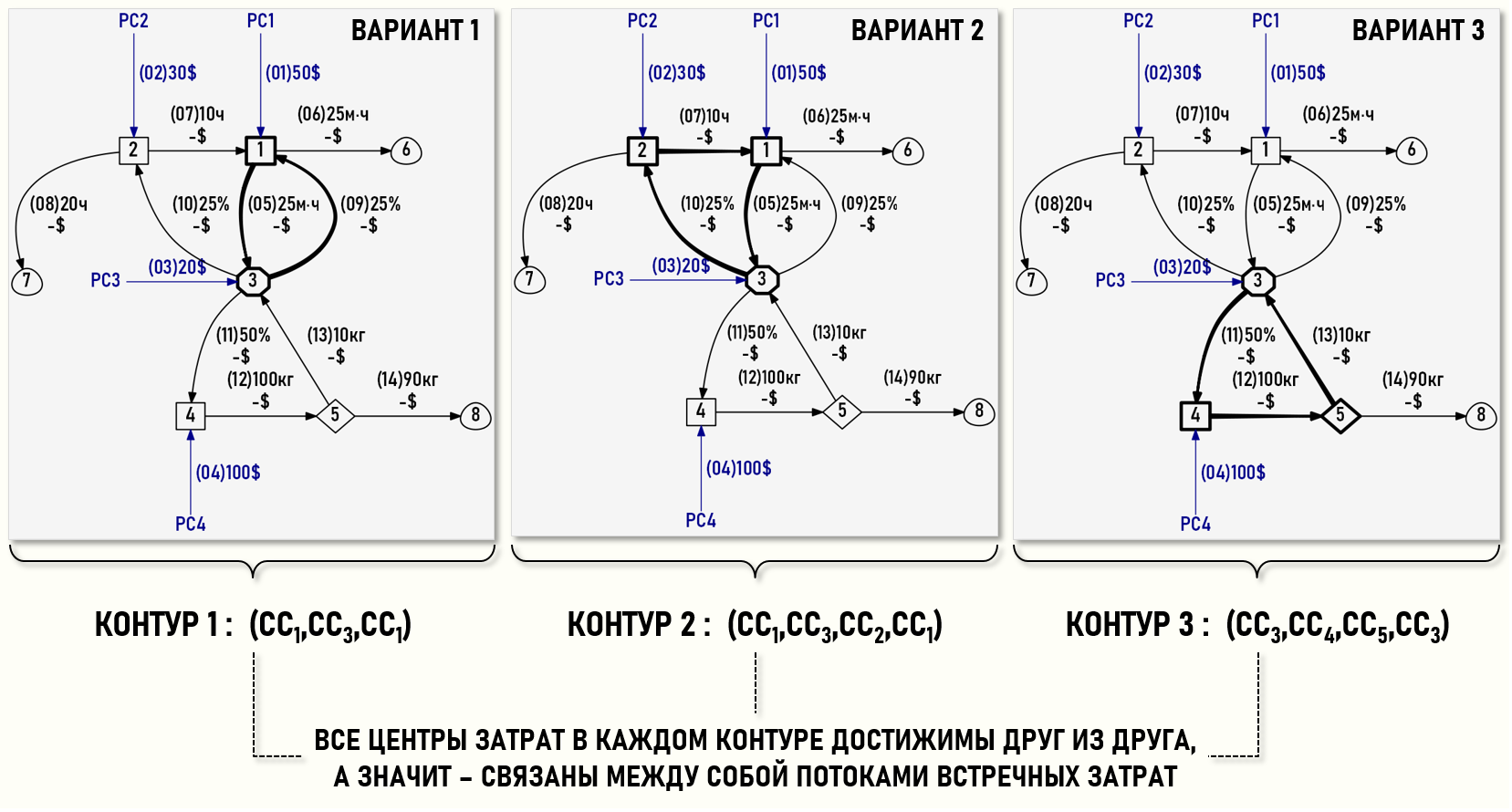
На рисунке в качестве примера представлены три варианта выделения встречных потоков затрат в изучаемом Графе затрат.
Вариант 1 представляет собой самую простую ситуацию, при которой Цех 1 (СС1) оказывает транспортные услуги Офису (СС3), который в свою очередь оказывает услуги управления Цеху 1 (СС1). В этом случае встречные потоки затрат отражаются двумя встречными дугами.
Вариант 2 несколько сложнее – Цех 1 (СС1) оказывает транспортные услуги Офису (СС3), который оказывает услуги управления Цеху 2 (СС2), выполняющему ремонтные работы для Цеха 1 (СС1). В этом случае встречные потоки затрат отражаются уже тремя дугами, причем встречными потоками затрат здесь попарно связаны все три центра затрат контура (CC1,CC3,CC2,CC1), поскольку все центры затрат контура достижимы друг из друга.
Вариант 3 аналогичен Варианту 2, но здесь в контур объединены другие центры затрат – (CC3,CC4,CC5,CC3).
Таким образом, даже в небольшой модели хозяйственной деятельности предприятия могут существовать много встречных потоков затрат.
РЕШЕНИЕ СЛАУ (НАХОЖДЕНИЕ ТАРИФОВ) (наверх)
Общий вид СЛАУ в матричной форме для нашей задачи имеет следующий вид:
P[8,8] TUC[8]=Z[8]
где:
P[8,8] – матрица коэффициентов уравнений
TUC[8] – вектор-столбец тарифов
Z[8] – вектор-столбец правых частей уравнений
Целью решения СЛАУ является нахождение вектора-столбца тарифов TUC[8]:
TUC[8]=P-1[8,8] Z[8]
где:
P-1[8,8] – обратная матрица коэффициентов уравнений
Для решения полученной СЛАУ надо найти обратную матрицу коэффициентов уравнений P-1[8,8] и умножить ее на вектор-столбец Z[8], в результате будет найден искомый вектор-столбец тарифов TUC[8]. Умножив далее полученные тарифы на количества единиц калькуляции можно будет найти стоимости хозяйственных операций с 5-ой по 14-ю.
В статье будет использован вариант формирования входящих в СЛАУ матриц, основанный на понижении размерности задачи за счет исключения из СЛАУ уравнений для центров затрат {CC6,CC7,CC8}, которые являются стоками и используются для формирования себестоимостей проданных транспортных услуг, ремонтных работ и продукции.
Рассмотрим подробнее процедуру решения СЛАУ с помощью типового функционала Microsoft Excel (скачать таблицы).
Для начала представим полученную СЛАУ в более удобном для практической работы виде – с помощью расширенной матрицы исходных коэффициентов PEXP[9,8], состоящей из квадратной матрицы коэффициентов уравнений P[8,8] и присоединенного к ней справа вектора-столбца правых частей уравнений Z[8]. Работа с таблицами Microsoft Excel предполагает свои особенности – все пустые ячейки матрицы PEXP[9,8] необходимо заполнить 0-ми из-за технологических особенностей вычисления некоторых функций.
На рисунке также показана и расширенная матрица исходных коэффициентов KEXP[9,8], которая не присутствует в явном виде в СЛАУ, но очень удобна для практической работы, т.к. позволяет в наглядной и компактной форме представить всю необходимую для распределения вторичных затрат информацию. Эту матрицу можно рассматривать в качестве «интерфейса» модели для расчета себестоимости.
Представив СЛАУ в «обычной» форме, можно увидеть, что уравнения 6, 7 и 8 фактически не нужны, т.к. тарифы {tUC6,tUC7,tUC8} используются только в «своих» уравнениях и не влияют на расчет значений остальных тарифов.
Это позволяет уменьшить число уравнений в СЛАУ с 8-ми до 5-ти. Исключив из рассмотрения столбцы и строки для стоков {CC6,CC7,CC8} преобразуем матрицу РEXP[9,8] в матрицу меньшей размерности – РEXP[6,5]:
Вычисленное в ячейке C20 значение определителя матрицы Р[5,5] отлично от 0-ля:
∆(5,5)=МОПРЕД(C15:G19)=-1,2×109≠0
Можно продолжить поиск единственного решения СЛАУ.
После уменьшения размерности задачи формула для нахождения значений тарифов примет следующий вид:
TUC[5]=P-1[5,5] Z[5]
Для нахождения обратной матрицы коэффициентов уравнений Р-1[5,5] воспользуемся функцией Microsoft Excel МОБР(), которая вводится как формула массива, предполагающая выполнение следующих действий:
- в ячейку N15 вводится формула МОБР(C15:G19)
- выделяется курсором область ячеек (N15:R19)
- не отменяя выделения ячеек области нажимается клавиша F2
- одновременно нажимается комбинация клавиш Shift+Ctrl+Enter
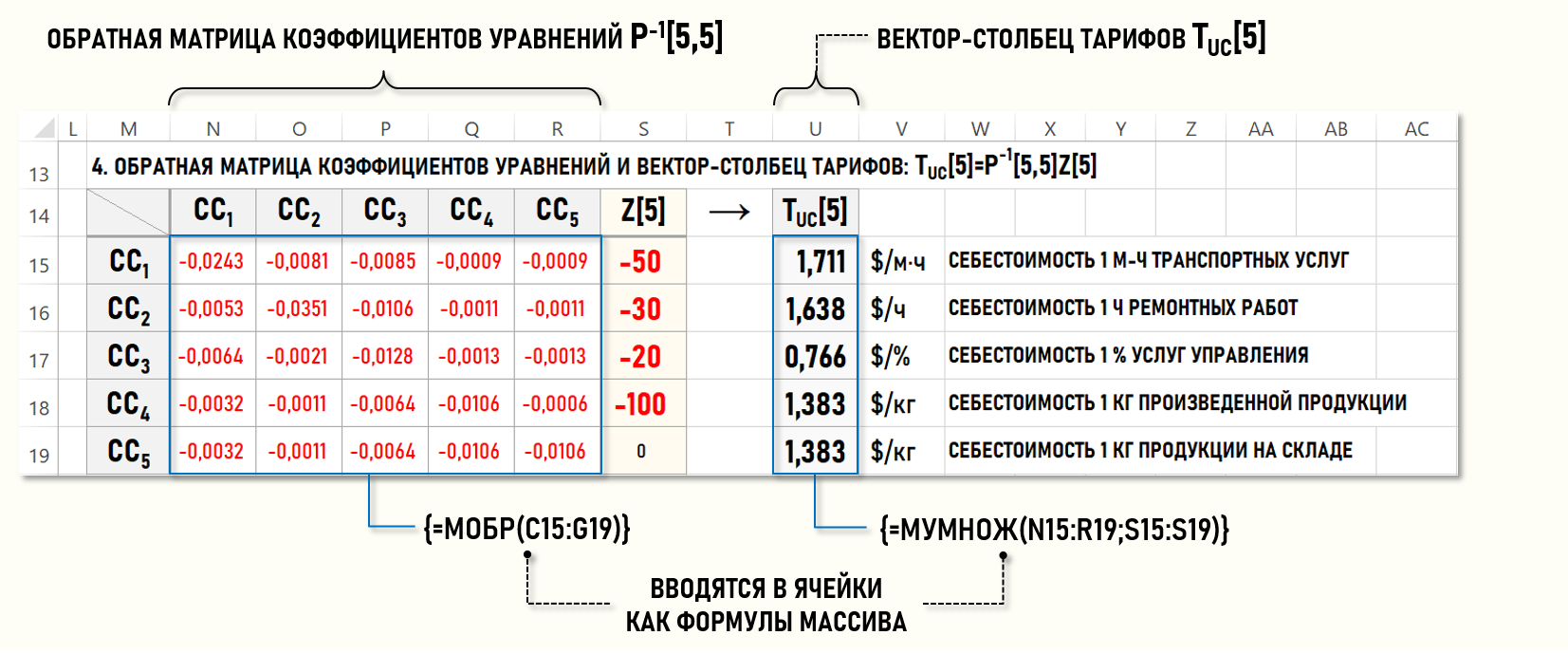
В результате в области ячеек (N15:R19) будет сформирована обратная матрица коэффициентов уравнений P-1[5,5].
После этого обратная матрица Р-1[5,5] умножается на вектор-столбец Z[5] и определяются значения элементов вектора-столбца тарифов TUC[5].
Перемножение матриц производится функцией Microsoft Excel:
МУМНОЖ(N15:R19;S15:S19)
где:
(N15:R19) – обратная матрица коэффициентов уравнений Р-1[5,5]
(S15:S19) – вектор-столбец правых частей уравнений Z[5]
Данная функция вводится как формула массива:
- в ячейку U15 вводится формула МУМНОЖ(N15:R19;S15:S19)
- выделяется курсором область ячеек (U15:U19)
- не отменяя выделения ячеек области нажимается клавиша F2
- одновременно нажимается комбинация клавиш Shift+Ctrl+Enter
В результате в области ячеек (U15:U19) сформируются искомые значения тарифов, т.е. будет найдено решение СЛАУ.
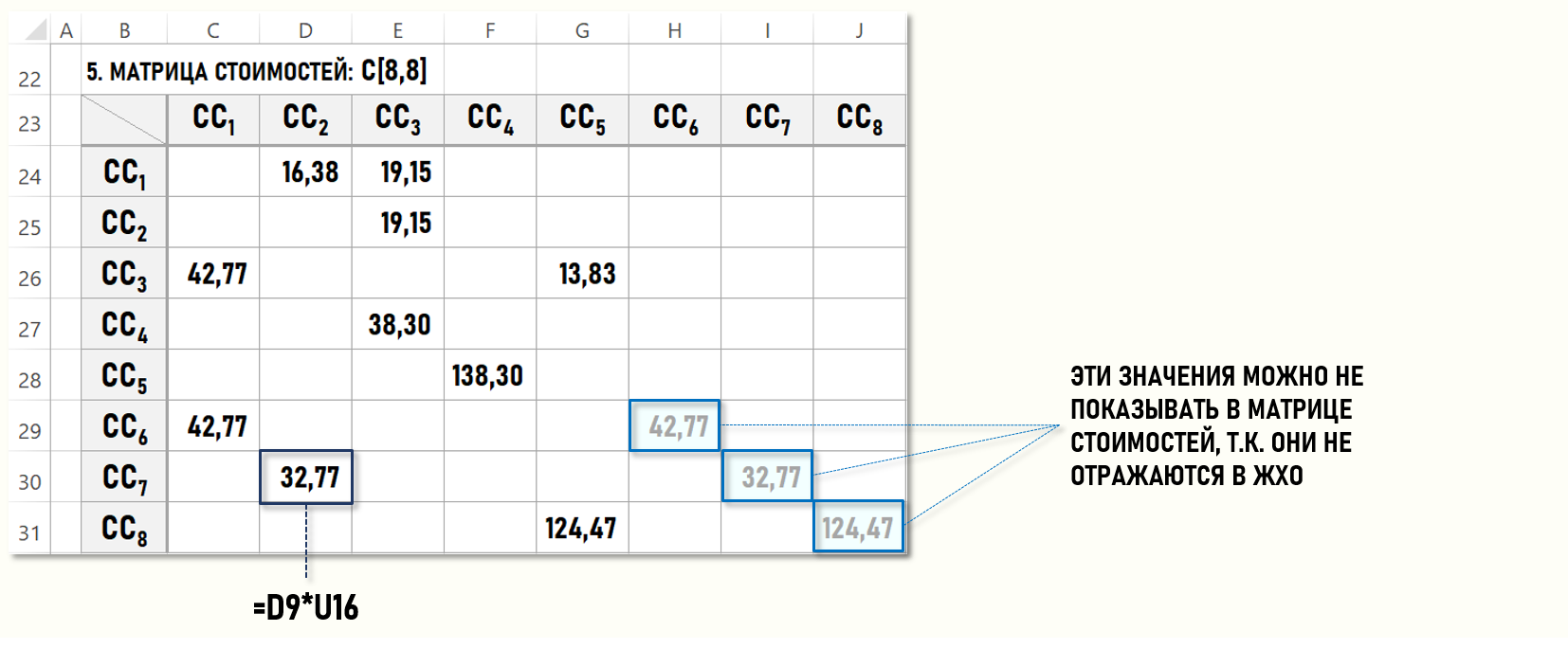
Теперь осталось определить значения элементов матрицы стоимостей C[8,8], для чего надо умножить значения элементов матрицы исходных коэффициентов К[8,8] на соответствующие значения тарифов из вектора-столбца ТUC[5].
В ячейках матрицы стоимостей C[8,8] содержатся все стоимости вторичных затрат, т.е. стоимости хозяйственных операций с 5-ой по 14-ю, которые теперь можно записать в ЖХО, как и значения тарифов:
Также представим множество хозяйственных операций в виде нарисованного Графа затрат, весами дуг которого являются номера операций из ЖХО (в скобках), количества единиц калькуляции и суммы операций.
ПРОВЕРКА РЕШЕНИЯ СЛАУ (наверх)
Проверим, выполняются ли уравнения баланса затрат для всех центров затрат нашего Графа затрат?
В «обычном» виде СЛАУ будет выглядеть следующим образом:
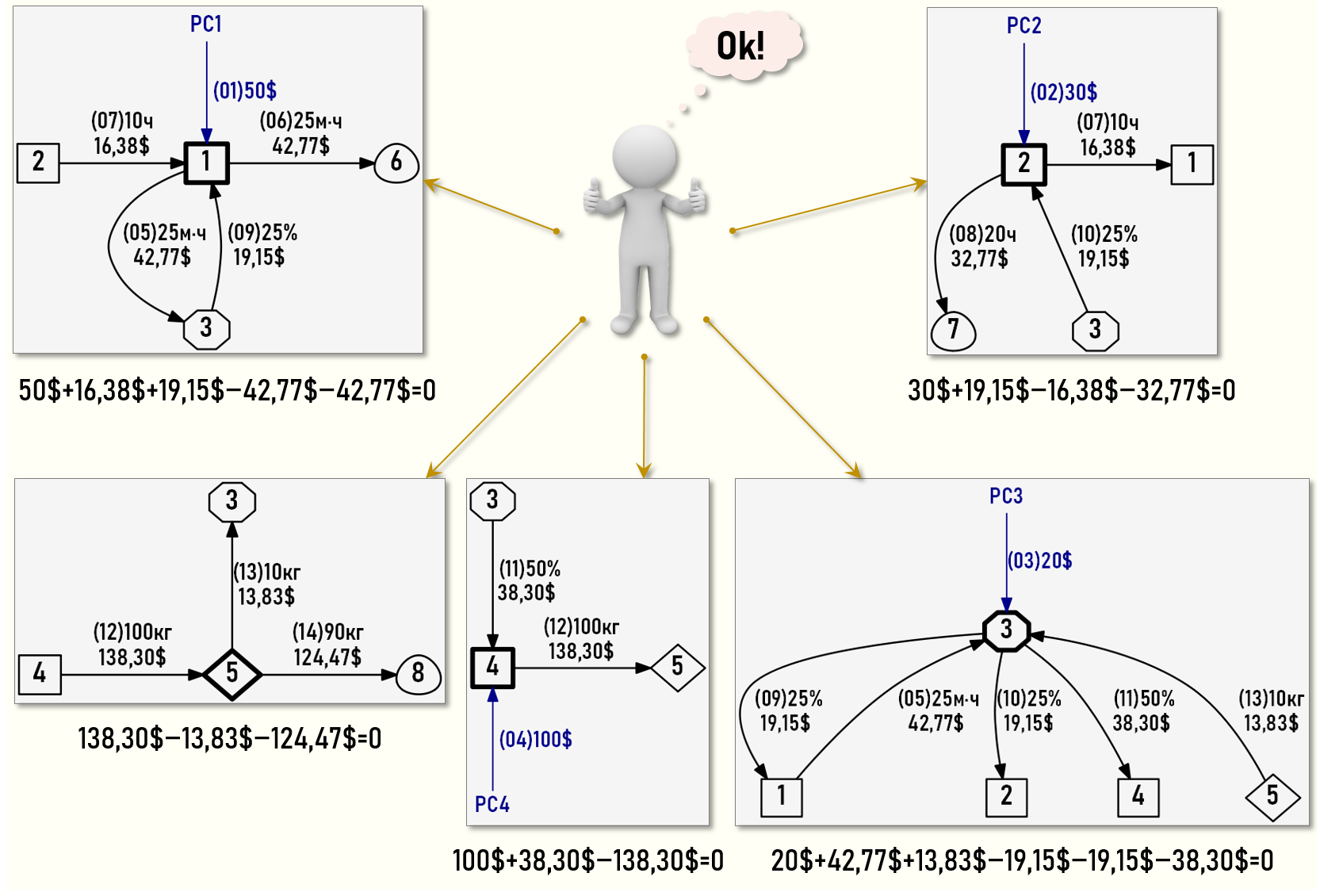
Представим также потоки затрат для каждого центра затрат в геометрической форме:
Как видно на рисунке, уравнения баланса затрат выполняются для всех центров затрат, т.е. расчет себестоимости выполнен математически корректно.
ВЫВОД:
Из вышеизложенного можно сделать вывод о том, что наличие встречных потоков затрат никак не сказалось на «технике» расчета себестоимости, т.е. в этом случае в процедуру расчета себестоимости с помощью решения СЛАУ не требуется вносить каких-либо изменений. Более того, производя расчет себестоимости, учетный специалист может не обращать внимания (или даже не знать) о существовании встречных затрат в модели, если решаемая задача не предполагает их анализа.