Расчет себестоимости (СЛАУ). Весовые коэффициенты
Автор: Александр Поляков
В данной статье мы рассмотрим вопрос, который от специалистов по расчету себестоимости можно услышать не просто часто, а очень часто. Формулируется он обычно так – у нас на предприятии есть подразделения, которые в одном и том же периоде производят несколько видов продукции, работ и услуг. Как рассчитать себестоимость в этом случае?
Выбор условной единицы калькуляции
Формирование СЛАУ в матричной форме
Решение СЛАУ (нахождение тарифов)
ОПИСАНИЕ СИТУАЦИИ (↑)
С ситуацией расчета себестоимости для случая, когда подразделение предприятия производит несколько видов продукции в одном и том же периоде, рано или поздно сталкивается каждый специалист по расчету себестоимости. Поэтому необходимо выяснить, почему возникают такие ситуации, когда от них можно уйти при расчете себестоимости, а когда уйти не получится, и что в этом случае делать?
Напомним, что в модели для расчета себестоимости – Графе затрат любой центр затрат является для пользователя «черным ящиком», внутренние процессы которого пользователю недоступны для наблюдения. Пользователь не может увидеть, каким образом внутри центра затрат происходит превращение входящих потоков затрат в исходящие потоки затрат, т.е. как делится стоимость входящих потоков затрат между исходящими потоками затрат, особенно в случае выпуска разных видов продукции, работ и услуг. Пользователь видит только, что на вход центра затрат поступили первичные и вторичные затраты, а на выходе появились вторичные затраты, относящиеся к разным видам продукции. В математической модели для расчета себестоимости стоимости этих исходящих вторичных затрат определяются с помощью единиц калькуляции разного вида, которые имеют разные стоимости (тарифы).
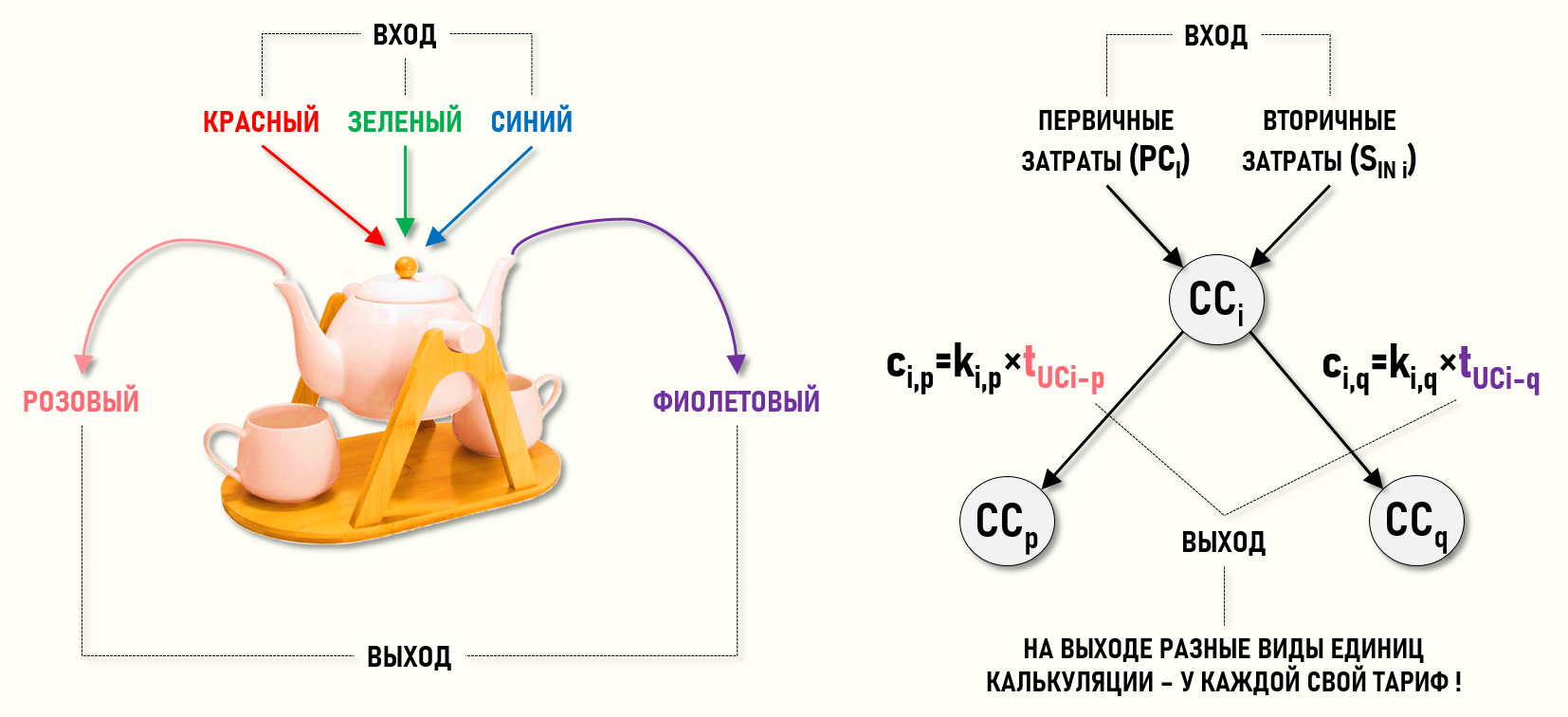
Здесь можно предложить такую наглядную аналогию. Возьмем чайник с двумя носиками, и нальем в него жидкости трех цветов – красного (R), зеленого (G) и синего (B). А потом нальем из одного носика в чашку жидкость розового цвета, а из другого носика в другую чашку жидкость фиолетового цвета. Как такое может быть?
Смешанные внутри чайника в определенных пропорциях жидкости этих трех цветов (RGB) могут дать на выходе любой заранее заданный цвет, но у нашего чайника из каждого носика выливается жидкость своего цвета – розовая и фиолетовая. Это может означать только одно – внутри чайника произошли какие-то более сложные процессы, чем простое перемешивание жидкостей трех базовых цветов в одной общей емкости. Возможно внутри чайника присутствует система перегородок, ограничивающих полости, в которых жидкости перемешиваются в разных пропорциях и образуют разные цвета, но в виду непрозрачности материала стенок чайника увидеть эти внутренние процессы не представляется возможным. Внешний наблюдатель видит только конечный результат смешивания жидкостей, когда из одного носика выливается розовая жидкость, а из другого – фиолетовая. Для того, чтобы узнать, как получился такой результат, необходимо получить дополнительную информацию, например, заглянуть внутрь чайника.
Аналогичная ситуация при определенных условиях может иметь место и в центрах затрат Графа затрат. Выше на рисунке пользователь модели, как внешний наблюдатель, видит на выходе центра затрат CCi потоки затрат, соответствующие разным видам продукции, работ или услуг. На вход центра затрат CCp уходит поток затрат, стоимость которого рассчитывается с помощью тарифа tUCi-p, а на вход центра затрат CCq уходит поток затрат, стоимость которого рассчитывается с помощью тарифа tUCi-q.
Для того, чтобы понять, как на выходе центра затрат CCi получаются разные тарифы для разных видов продукции, работ или услуг, пользователю необходимо получить дополнительную информацию, например, «заглянуть» внутрь центра затрат. А это означает, что данная модель просто не соответствует ожиданиям пользователя, она слишком приблизительная (грубая) для тех задач, которые он хочет решать с ее помощью. В этом случае желательно построить более подробную модель, в которой будут видны все хозяйственные процессы, имеющие место внутри исходного центра затрат.
Например, можно разделить исходный центр затрат на несколько центров затрат и показать в явном виде ранее скрытые от пользователя «внутренние» потоки затрат исходного центра затрат, т.е. сделать доступными для наблюдения хозяйственные процессы внутри исходного центра затрат.
Если вопросы не исчезнут, то модель необходимо усложнять дальше. Путем подобных итераций можно уточнять модель до тех пор, пока пользователь не решит, что для решения его задачи дальше уже нет нужды в получении более подробного Графа затрат. Основная задача – построить модель так, чтобы на выходе каждого центра затрат был бы только один вид единицы калькуляции. Это необходимое условие для решения задач на Графе затрат, т.к. только в этом случае эффективно начнут работать уравнения баланса затрат для расчета себестоимости.
Однако, на практике часто по тем или иным причинам, зависящим или не зависящим от разработчика модели, в Графе затрат все-таки остаются отдельные центры затрат, на выходе которых существуют единицы калькуляции разного вида.
Например, когда из полиметаллической руды, содержащей несколько видов драгоценных металлов, пытаются выделить золото и серебро, то довольно долго эти два металла идут по цепочке технологического процесса вместе, как составляющие одного концентрата. Учет драгоценных металлов производится на каждом переделе не в тоннах руды или концентрата, а в граммах содержащихся в них драгоценных металлов путем измерения их содержания в концентрате. Получается, что на выходе отдельных переделов золото и серебро идут вместе, а затраты на их получение необходимо считать раздельно. Такая же ситуация возникает и с попутным природным газом, который выходит на поверхность одновременно с добычей нефти, и еще в ряде подобных случаев.
Практика моделирования предусматривает еще одну ситуацию, при которой в Графе затрат могут быть использованы центры затрат, выпускающие несколько видов продукции, работ и услуг. Данная ситуация возникает тогда, когда технологический процесс предприятия позволяет выбрать на выходе каждого центра затрат только один вид единицы калькуляции, но(!) разработчик Графа затрат по каким-либо причинам не использует эту возможность.
Часто это обусловлено сознательным желанием пользователя модели не увеличивать порядок Графа затрат из-за неминуемого повышения трудоемкости учета затрат, а значит и рабочей нагрузки на пользователей системы учета. Увеличение размера модели может потребовать увеличения объема дополнительных аналитических данных, которые необходимо будет вводить в автоматизированную систему учета, становится сложнее контролировать логическую целостность модели, труднее разбираться с ошибками, возникающими во время проведения процедуры расчета себестоимости. Иногда это действительно может явиться непреодолимым препятствием для успешного внедрения спроектированного Графа затрат и заставить разработчика пересмотреть топологию Графа затрат в сторону ее упрощения.
Таким образом, достаточно часто возникают ситуации, когда не удается (или экономически нецелесообразно) построить очень подробные модели предприятий для расчета себестоимости. Что в этом случае делать? И вот здесь может помочь алгоритм A-W-C, называемый также методом весовых коэффициентов, который мы и рассмотрим далее на примере.
Далее будет рассмотрена процедура расчета себестоимости, основанная на решении системы линейных алгебраических уравнений (СЛАУ) с помощью типового функционала Microsoft Excel. Изучение этой процедуры будет происходить на примере небольшого производственного предприятия. Рекомендуется скачать таблицы Microsoft Excel для рассматриваемого примера и работать с ними в процессе изучения материала статьи.
УСЛОВИЯ ЗАДАЧИ (↑)
Рассмотрим небольшое лесопильное предприятие (лесопилку), состоящее из двух цехов и офиса, в котором сосредоточен административный персонал. Лесопилка имеет свою дизельную электростанцию (Цех 1), которая снабжает электроэнергией Цех 2, производящий доски, а также Офис, в котором сосредоточен административный персонал. Часть электроэнергии продается сторонним потребителям.
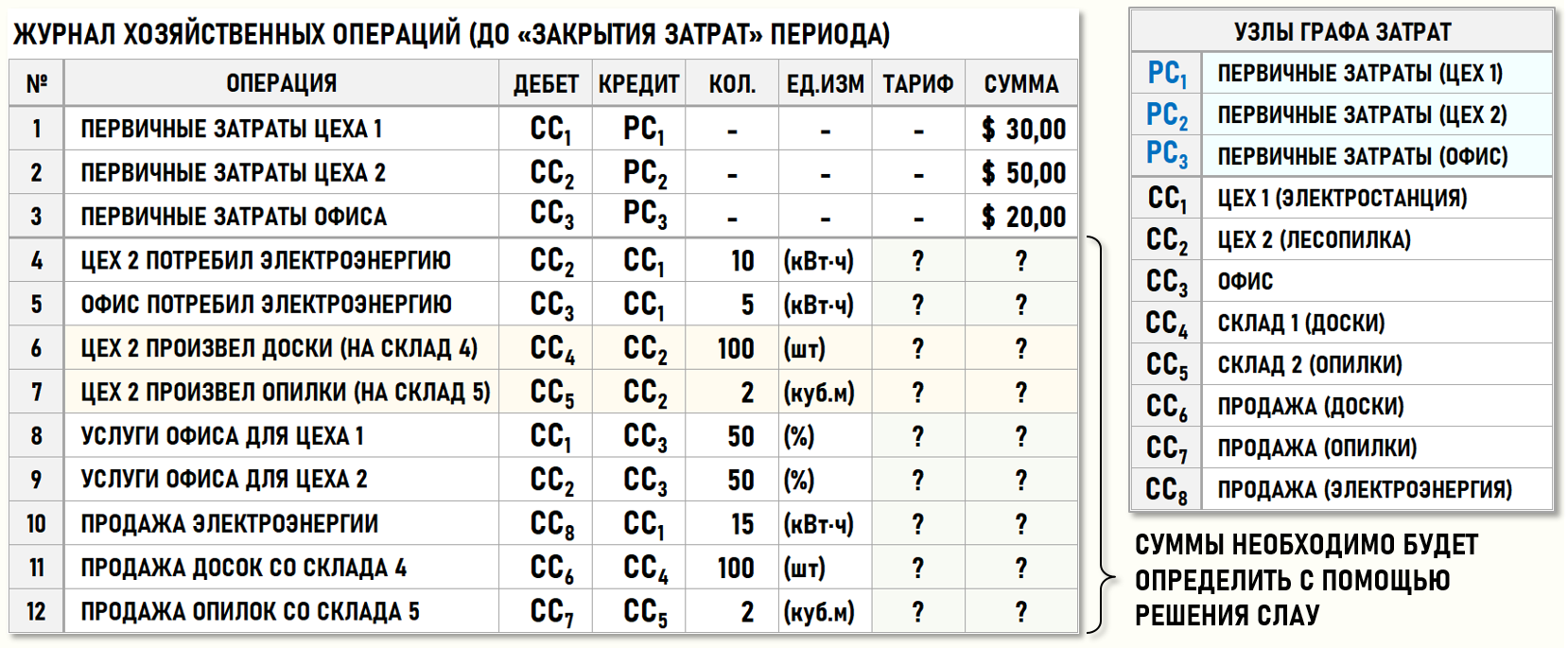
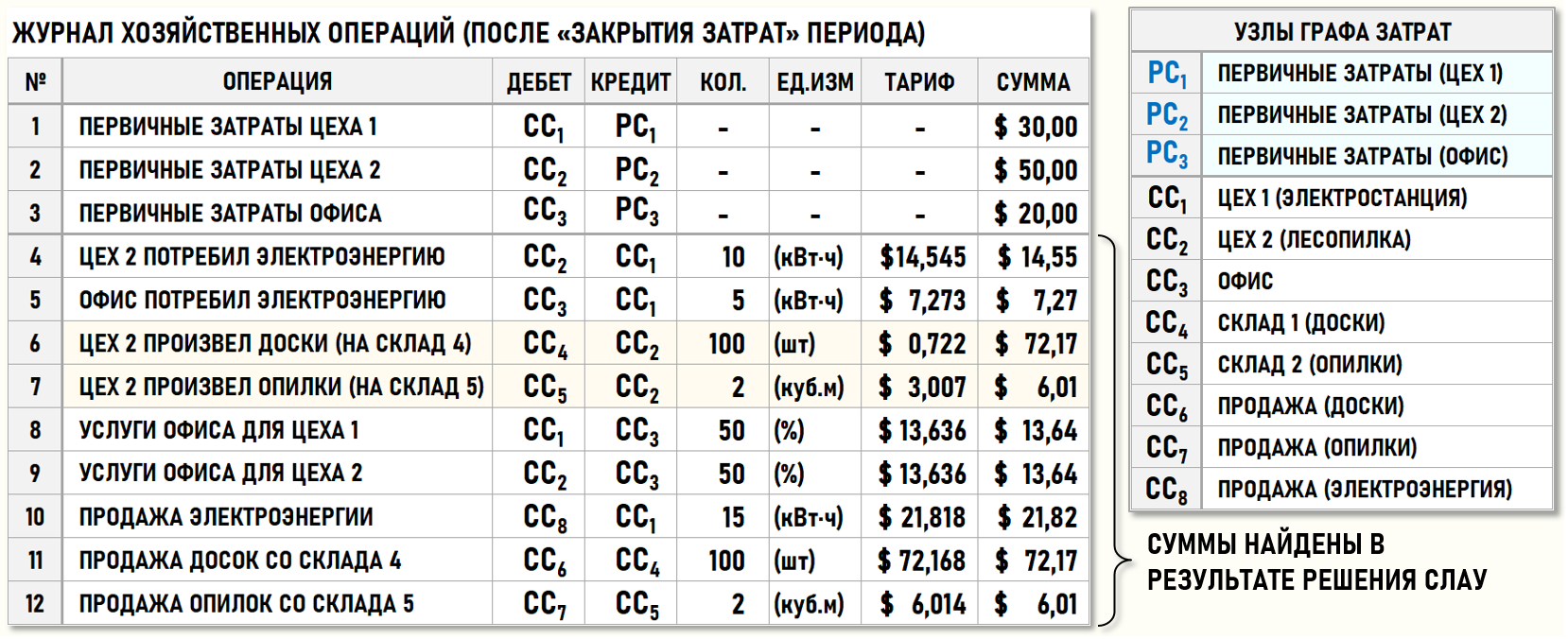
Ниже на рисунке представлен журнал хозяйственных операций (ЖХО) предприятия за отчетный период:
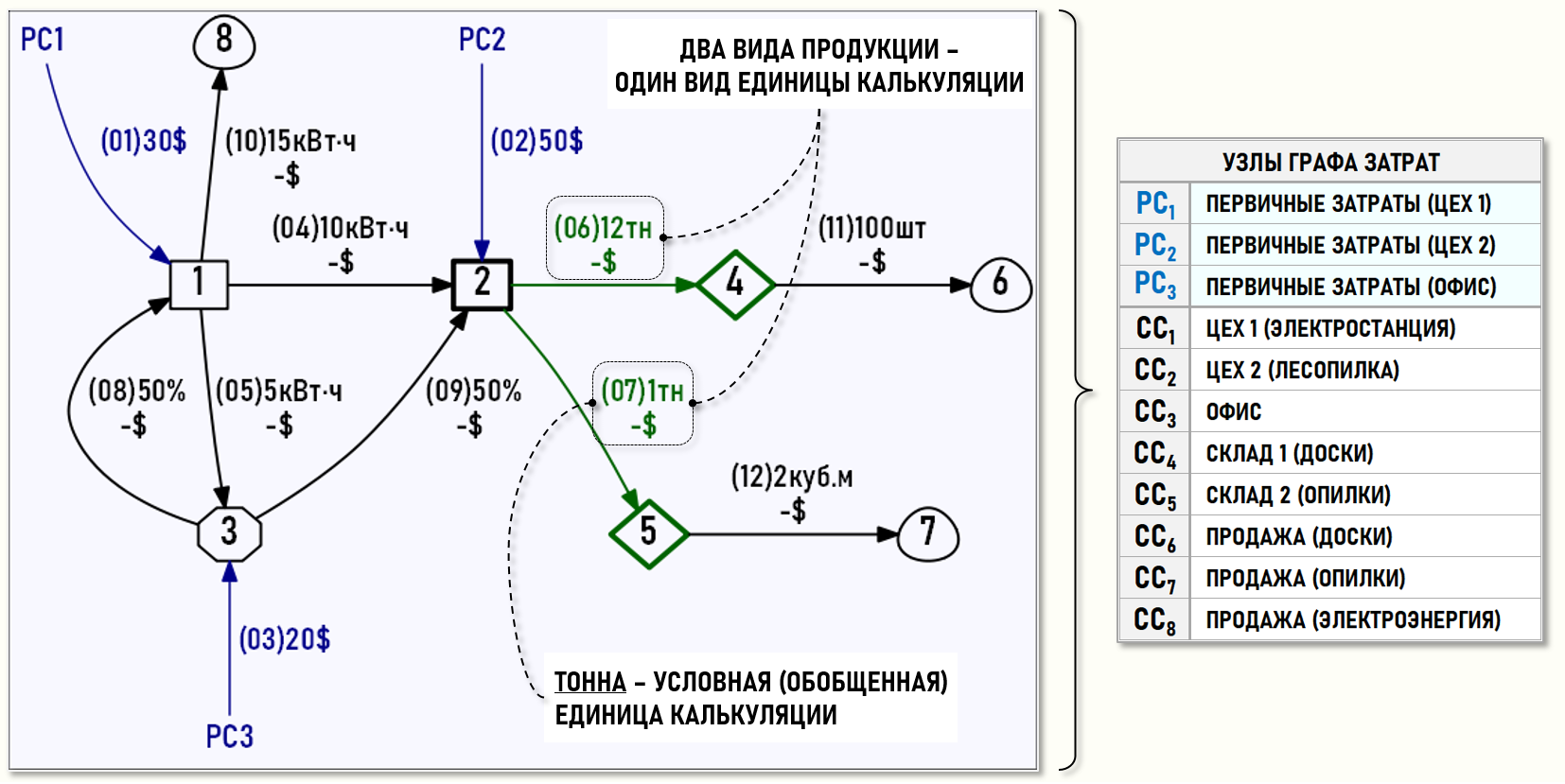
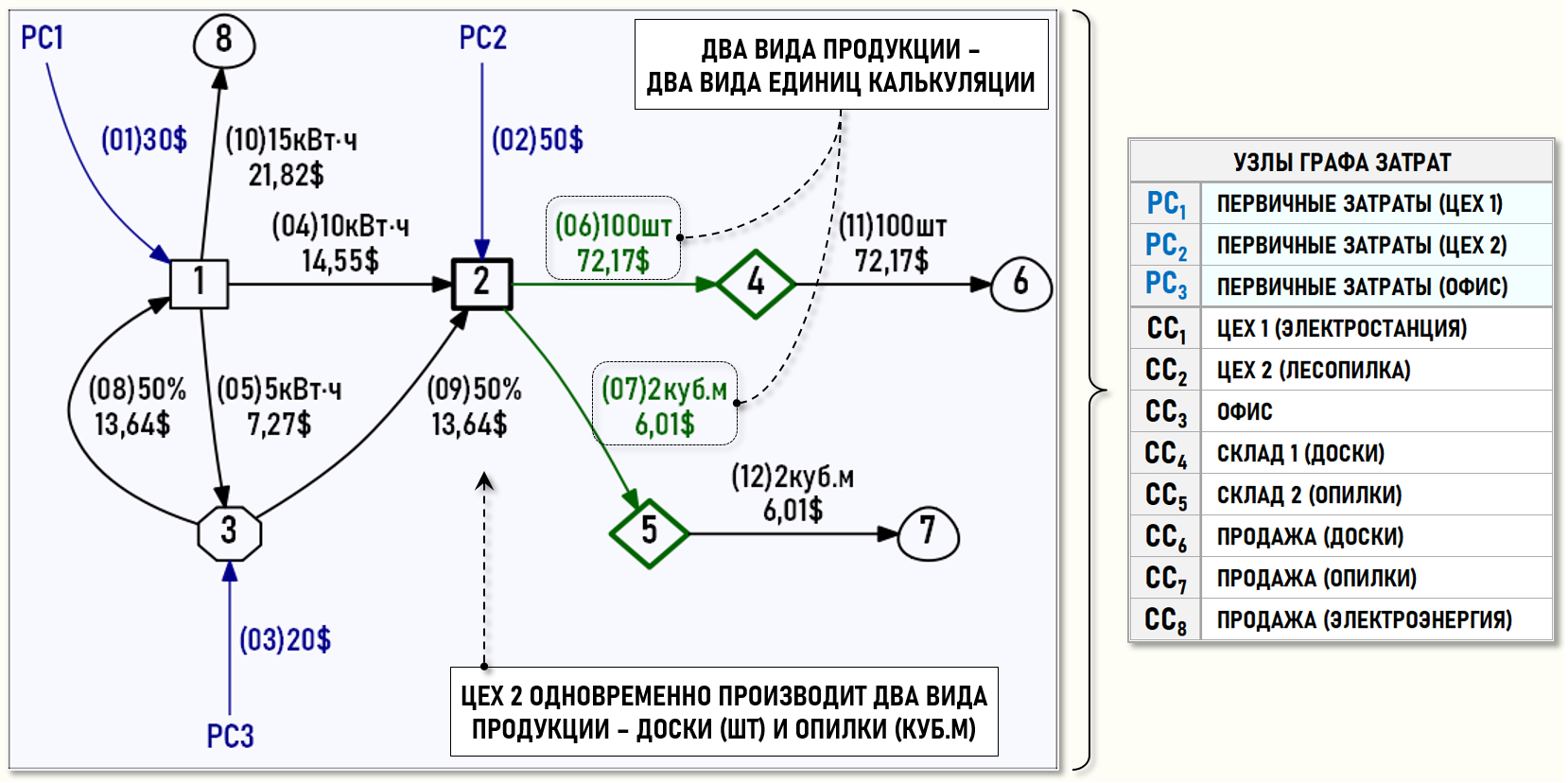
Также представим множество хозяйственных операций отчетного периода в геометрической форме, т.е. в виде нарисованного Графа затрат, дуги которого идентифицируются номерами хозяйственных операций (в скобках), весами дуг выступают количества единиц калькуляции и суммы хозяйственных операций.
Дизельная электростанция Цеха 1 (СС1) произвела в отчетном периоде 30 кВт·ч электроэнергии. Цех 2 (СС2) потребил 10 кВт·ч, Офис (СС3) потребил 5 кВт·ч, продано сторонним потребителям 15 кВт·ч электроэнергии. Себестоимость проданной электроэнергии формируется на входе центра затрат СС8.
Цех 2 (СС2) в отчетном периоде произвел и поместил на Склад 4 (СС4) 100 досок. В процессе производства досок образовалось 2 куб.м опилок, которые были помещены на Склад 5 (СС5). Все произведенные за отчетный период доски и опилки были проданы покупателям. Себестоимость проданных досок формируется на входе центра затрат СС6, себестоимость проданных опилок формируется на входе центра затрат СС7.
Как известно, производство досок сопровождается получением опилок, которые в общем случае рассматриваются как «обычный» вид продукции, такой же, как и доски, поскольку опилки могут являться не только отходами производства, но и ценным сырьем для производства топливных брикетов. В нашем примере доски и полученные при их производстве опилки считаются «равноправными» видами продукции, производство которых Цехом 2 (CC2) по понятным причинам происходит одновременно. Далее каждый вид продукции поступает на свой склад и продается покупателям.
Управление деятельностью предприятия производится административным персоналом в Офисе (СС3). Распределение стоимости управленческих затрат между цехами производится в равных долях (по 50%). В данном случае рассчитываются полные себестоимости проданных электроэнергии, досок и опилок – в них включаются стоимости затрат на управление предприятием.
Пока не будет выполнена процедура закрытия затрат периода, только три хозяйственные операции (с 1-ой по 3-ю) будут иметь не 0-вые стоимости. Остальные хозяйственные операции (с 4-ой по 12-ю) характеризуются пока только количествами единиц калькуляции, которые всегда известны до начала процедуры закрытия затрат периода. Стоимости этих хозяйственных операций будут определены по результатам выполнения процедуры расчета себестоимости – закрытия затрат периода.
ВЫБОР УСЛОВНОЙ ЕДИНИЦЫ КАЛЬКУЛЯЦИИ (↑)
На выходе Цеха 2 (CC2) мы видим единицы калькуляции двух видов – доски (100 шт) и опилки (2 куб.м), но для того, чтобы воспользоваться уравнениями баланса затрат для расчета себестоимости, нам необходимо получить только один вид единицы калькуляции.
Эту проблему можно решить с помощью метода весовых коэффициентов, идея которого заключается в том, что, опираясь на дополнительную информацию о производимых видах продукции, все исходные единицы калькуляции приводятся к некоей условной (обобщенной) единице калькуляции, применение которой и позволяет составить уравнение баланса затрат для центра затрат.
При выборе условной единицы калькуляции многое зависит от того, насколько хорошо разработчик модели знаком с тонкостями производственного процесса, это позволяет подобрать наиболее адекватный вид общей единицы измерения для различных видов продуктов, работ и услуг. Надо понимать, что это всегда процесс поиска наилучшего приближения к реальной хозяйственной ситуации, при котором пользователь может выбирать условную единицу калькуляции из спектра возможных альтернатив. В зависимости от объема и качества дополнительной информации, а также исходя из профессионализма и субъективных предпочтений, разработчик может это сделать либо лучше, либо хуже, но в любом случае – это будет лишь некое приближение к реальности.
Какую условную единицу калькуляции можно выбрать для нашего примера? Какая дополнительная информация может пригодиться в данном случае?
Например, мы знаем, что доски и опилки изготовлены из сосны, а ее плотность известна (~0,5 тн/куб.м). Эта информация позволяет в качестве условной единицы калькуляции выбрать единицу массы (1 тн) досок и опилок в предположении о том, что опилки на складе очень плотно спрессованы, иначе их плотность будет значительно меньше плотности цельного куска сосны. Конечно, это определенное допущение, но, как было сказано выше, метод весовых коэффициентов лишь в каком-то приближении позволяет привести к единой единице измерения разные виды продукции, работ и услуг.
Зная плотность сосны, рассчитаем массу одной доски и 1-го куб.м опилок, это и будут весовые коэффициенты, позволяющие пересчитывать исходные единицы калькуляции в условные единицы калькуляции:
КW1=0,2 м × 0,2 м × 6 м × 0,5 тн/куб.м = 0,12 тн
КW2=1 куб.м × 0,5 тн/куб.м = 0,5 тн
где:
0,2 м – высота и ширина доски (бруса)
6 м – длина доски
Полученные весовые коэффициенты КW1 и КW2 показывают, на какое значение необходимо умножить количество исходных единиц калькуляции (штуки и куб.м) для того, чтобы перейти к значениям в условных единицах калькуляции (тонны).
В условиях задачи мы имеем следующие значения исходных коэффициентов на выходе Цеха 2 (CC2):
k2,4=100 шт – произведено 100 досок
k2,5=2 куб.м – произведено 2 куб.м опилок
Рассчитаем новые значения этих исходных коэффициентов, используя весовые коэффициенты KW1 и KW2:
k2,4 NEW=k2,4×KW1=100×0,12=12 тн – соответствует 100-та доскам
k2,5 NEW=k2,5×KW2=2×0,5=1 тн – соответствует 2-м куб.м опилок
Покажем полученные значения на Графе затрат:
Теперь продукция (доски и опилки) на выходе Цеха 2 (CC2) измеряется с помощью одной единицы калькуляции (тонны), т.е. можно продолжить расчет себестоимости с помощью математической модели, основанной на решении СЛАУ. Также необходимо отметить, что в нашем примере можно было выбрать и другой вид условной единицы калькуляции, например, измерить количество досок и опилок в единицах объема (куб.м). Как было сказано выше, у пользователя модели есть спектр возможных альтернатив.
ФОРМИРОВАНИЕ СЛАУ В МАТРИЧНОЙ ФОРМЕ (↑)
Общий вид СЛАУ в матричной форме для нашей задачи имеет следующий вид:
P[8,8] TUC[8]=Z[8]
где:
P[8,8] – матрица коэффициентов уравнений
TUC[8] – вектор-столбец тарифов
Z[8] – вектор-столбец правых частей уравнений
Целью решения СЛАУ является нахождение вектора-столбца тарифов ТUC[8]:
TUC[8]=P-1[8,8] Z[8]
где:
P-1[8,8] – обратная матрица коэффициентов уравнений
В статье будем использовать способ понижения размерности задачи за счет исключения из СЛАУ уравнений для центров затрат {CC6,CC7,CC8}, которые являются стоками и используются для формирования себестоимостей проданных досок, опилок и электроэнергии. Все затраты предприятия, попавшие в эти стоки, превращаются в расходы, т.е. эти центры затрат моделируют «факт выбытия» активов предприятия в результате их продажи покупателям.
Поскольку значения тарифов нужны для определения стоимости исходящих из центра затрат потоков вторичных затрат, а стоки никогда не отдают свои затраты другим центрам затрат, то искать значения тарифов для стоков особого смысла не имеет. В результате, уравнения баланса затрат для центров затрат {CC6,CC7,CC8} можно не учитывать при расчете себестоимости, т.е. количество уравнений баланса затрат в СЛАУ для нашей задачи может быть уменьшено с 8-ми до 5-ти.
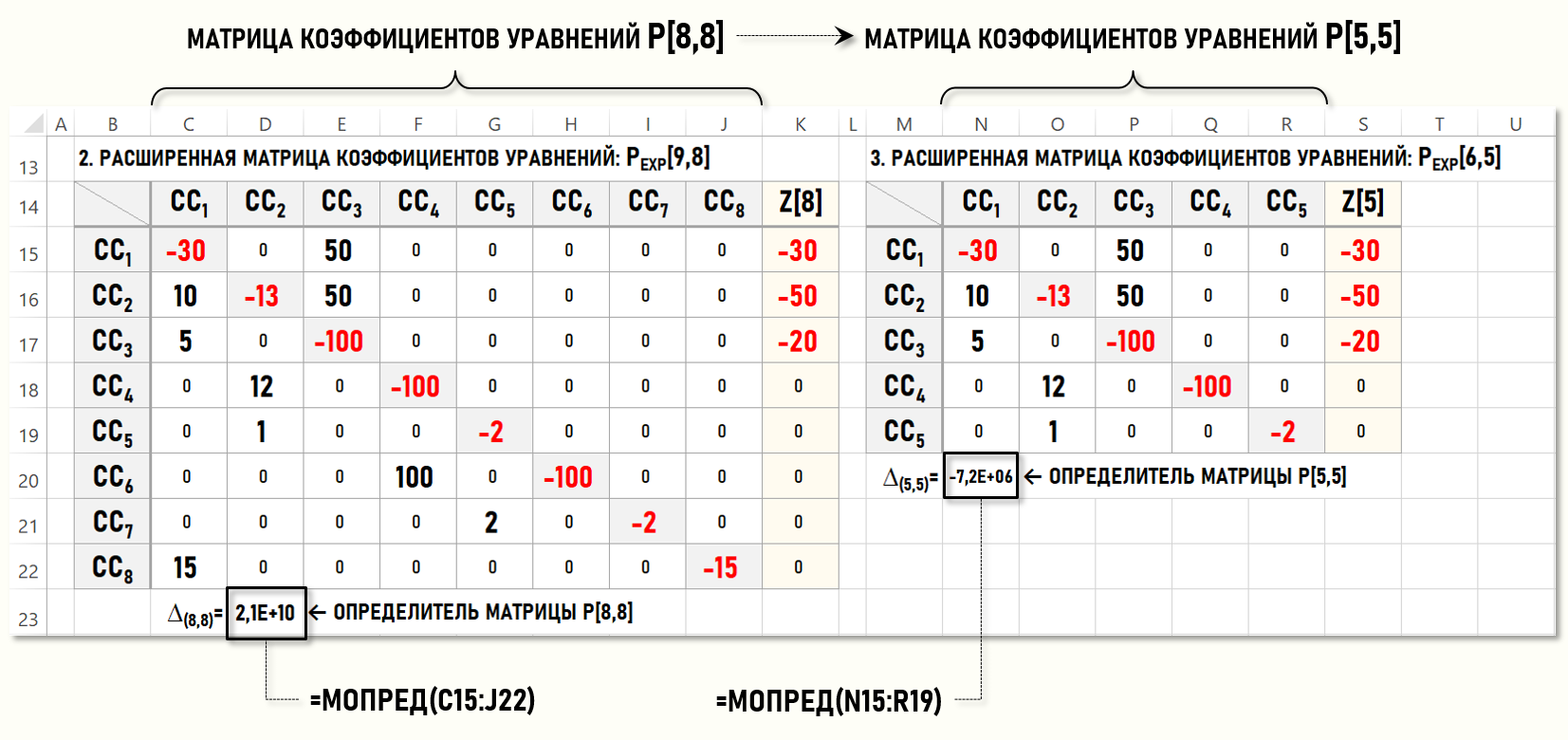
Рассмотрим процедуру решения СЛАУ с помощью типового функционала Microsoft Excel. После выбора условной единицы калькуляции для Цеха 2 (CC2) расширенная матрица исходных коэффициентов KEXP[9,8] примет следующий вид (правая матрица ниже на рисунке):
Изначально на выходе центра затрат CC2 было:
k2,4=100 (шт) досок
k2,5=2 (куб.м) опилок
После выбора условной единицы калькуляции на выходе центра затрат CC2 стало:
k2,4 NEW=12 (тн) досок
k2,5 NEW=1 (тн) опилок
Все остальные значения исходных коэффициентов остались без изменений. Причем, возникла интересная ситуация. На входе Склада 4 (CC4) и Склада 5 (CC5) продукция измеряется в тоннах, а на выходах этих центров затрат продукция измеряется в штуках и кубометрах. Другими словами, на склады поступают доски и опилки, измеряемые в условных единицах калькуляции (тн), а «уходят» со складов доски в штуках и опилки в кубометрах. Эта подмена единиц калькуляции действует только на время выполнения процедуры расчета себестоимости, после проведения которой необходимо опять вернуться к исходным единицам калькуляции – штукам и кубометрам.
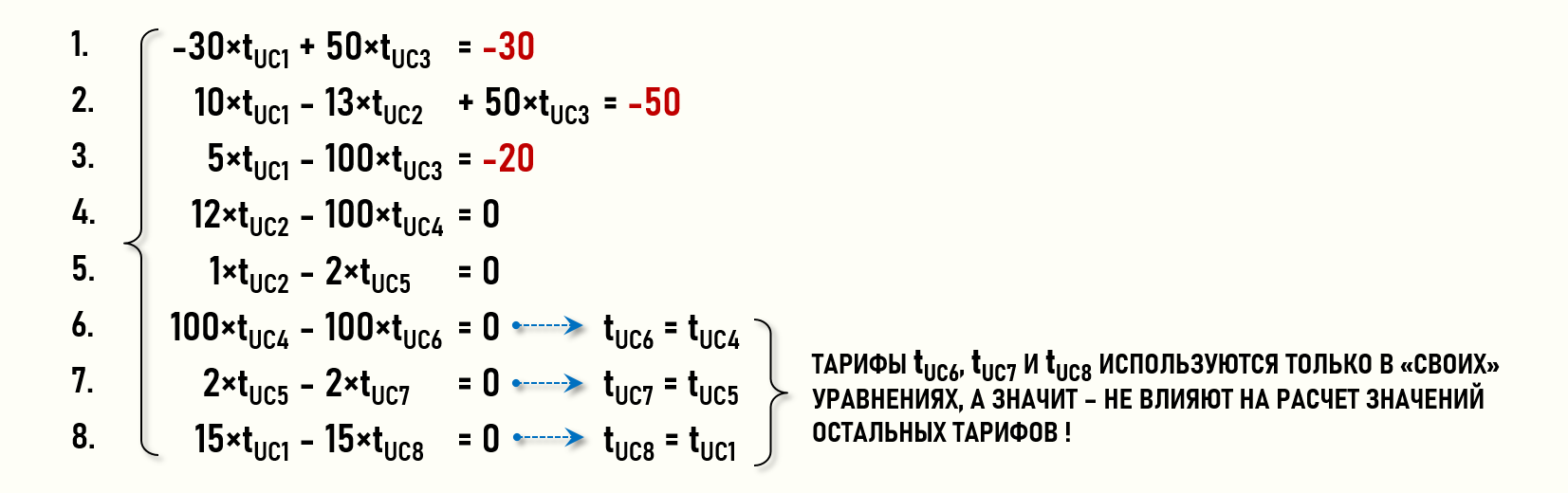
Если представить СЛАУ в «обычной» форме, то легко увидеть, что уравнения 6, 7 и 8 фактически не нужны, т.к. тарифы {tUC6,tUC7,tUC8} используются только в «своих» уравнениях, а значит – не влияют на расчет значений остальных тарифов.
Это позволяет уменьшить число уравнений в СЛАУ с 8-ми до 5-ти. Исключив из рассмотрения столбцы и строки для стоков {CC6,CC7,CC8}, преобразуем расширенную матрицу коэффициентов уравнений РEXP[9,8] в матрицу меньшей размерности – РEXP[6,5]:
Вычисленное в ячейке N20 значение определителя ∆(5,5) матрицы Р[5,5] отлично от 0-ля:
∆(5,5)=МОПРЕД(N15:R19)=-7,2×106≠0
Можно продолжить поиск единственного решения СЛАУ.
РЕШЕНИЕ СЛАУ (НАХОЖДЕНИЕ ТАРИФОВ) (↑)
После уменьшения размерности задачи формула для нахождения значений тарифов примет следующий вид:
Для нахождения обратной матрицы коэффициентов уравнений Р-1[5,5] воспользуемся функцией Microsoft Excel МОБР(), которая вводится как формула массива, предполагающая выполнение следующих действий:
- в ячейку C27 вводится формула МОБР(N15:R19)
- выделяется курсором область ячеек (C27:G31)
- не отменяя выделения ячеек области нажимается клавиша F2
- одновременно нажимается комбинация клавиш Shift+Ctrl+Enter
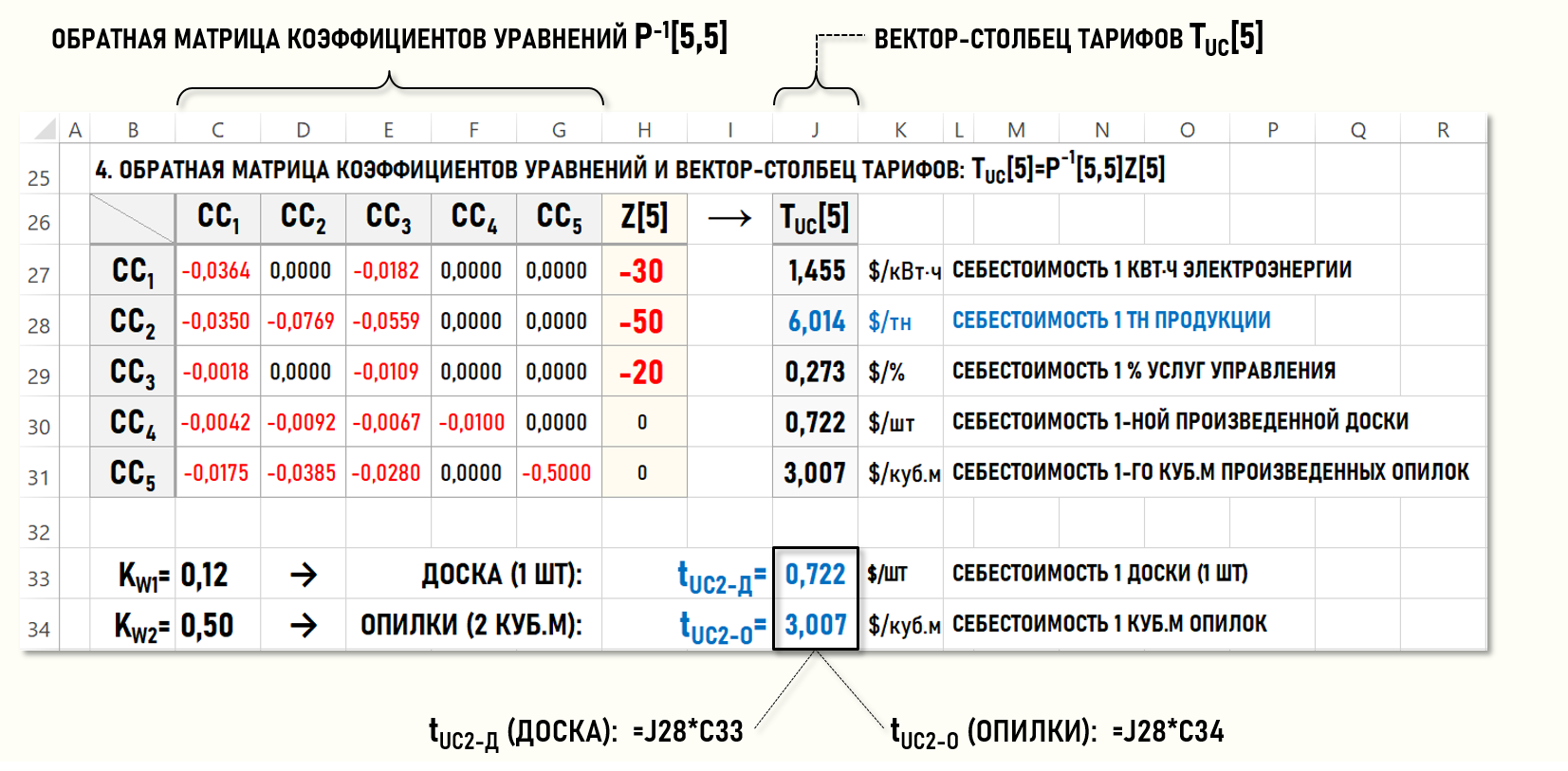
В результате в области ячеек (C27:G31) будет сформирована обратная матрица коэффициентов уравнений P-1[5,5].
После этого выполняется последний шаг процедуры решения СЛАУ – матрица Р-1[5,5] умножается на вектор-столбец Z[5] и определяются значения элементов вектора-столбца тарифов TUC[5]. Перемножение матриц производится функцией Microsoft Excel:
МУМНОЖ(C27:G31;H27:H31)
где:
(C27:G31) – обратная матрица коэффициентов уравнений Р-1[5,5]
(H27:H31) – вектор-столбец правых частей уравнений Z[5]
Данная функция вводится как формула массива:
- в ячейку J27 вводится формула МУМНОЖ(C27:G31;H27:H31)
- выделяется курсором область ячеек (J27:J31)
- не отменяя выделения ячеек области нажимается клавиша F2
- одновременно нажимается комбинация клавиш Shift+Ctrl+Enter
В результате в области ячеек (J27:J31) сформируются искомые значения тарифов, т.е. будет найдено решение СЛАУ.
Далее с помощью весовых коэффициентов KW1 и KW2 необходимо пересчитать значение тарифа tUC2 для условной единицы калькуляции в значения тарифов для исходных единиц калькуляции – одной доски и одного куб.м опилок:
tUC2-Д=tUC2×KW1=6,014×0,12=0,722 $/шт – себестоимость одной доски
tUC2-О=tUC2×KW2=6,014×0,50=3,007 $/куб.м – себестоимость 1-го куб.м опилок
МАТРИЦА СТОИМОСТЕЙ (↑)
Теперь осталось определить значения элементов матрицы стоимостей C[8,8], для чего надо умножить значения элементов матрицы исходных коэффициентов К[8,8] на соответствующие значения тарифов из вектора-столбца ТUC[5].
В ячейках матрицы стоимостей C[8,8] содержатся все стоимости вторичных затрат, т.е. стоимости хозяйственных операций с 4-ой по 12-ю, которые теперь можно записать в ЖХО, как и значения тарифов из вектора-столбца TUC[5]:
Также представим множество хозяйственных операций в виде нарисованного Графа затрат, весами дуг которого являются номера операций из ЖХО (в скобках), количества единиц калькуляции и суммы операций.
ПРОВЕРКА РЕШЕНИЯ СЛАУ (↑)
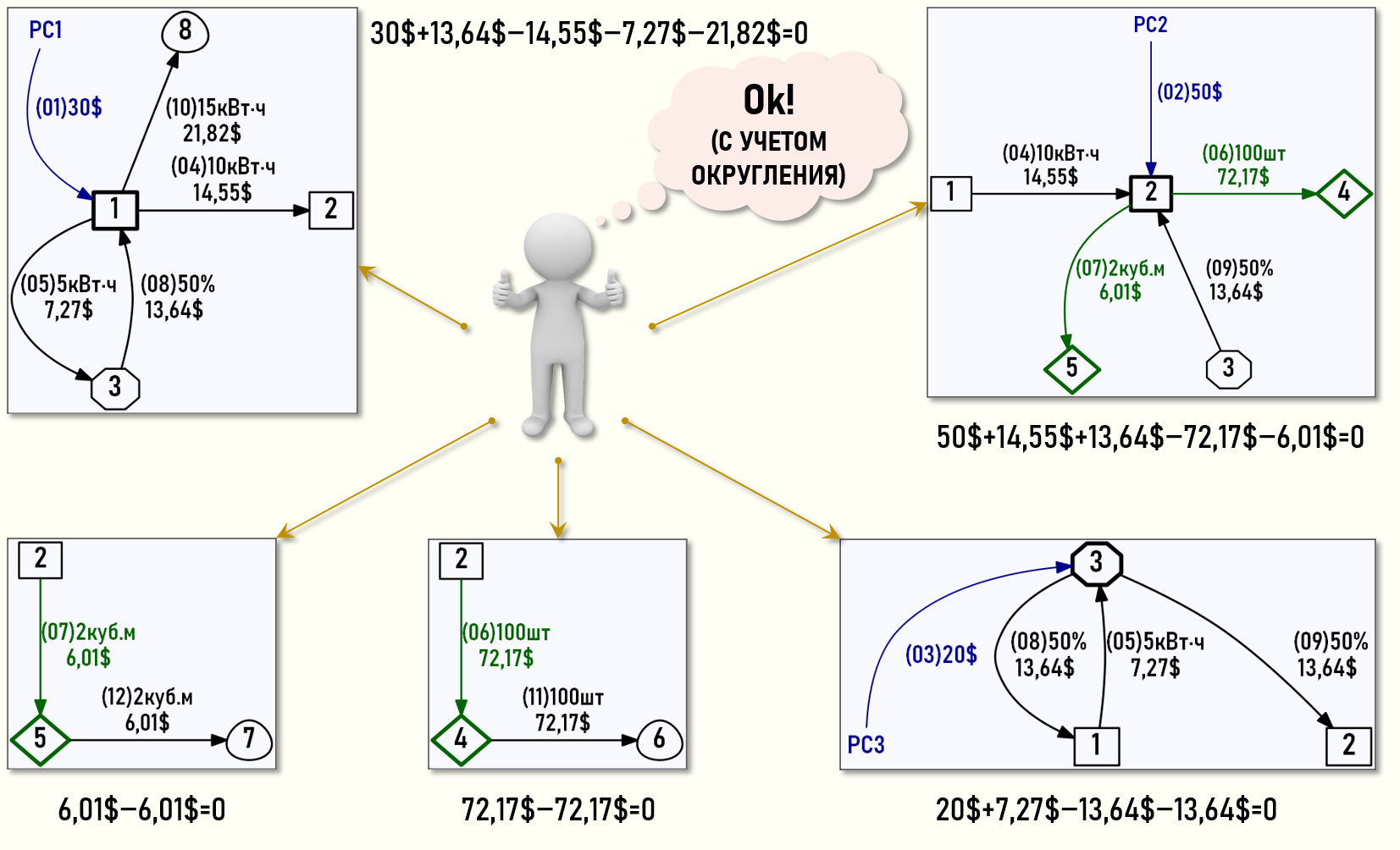
Проверим, выполняются ли уравнения баланса затрат для всех центров затрат нашего Графа затрат?
В «обычном» виде СЛАУ будет выглядеть следующим образом:
Представим также потоки затрат для каждого центра затрат в геометрической форме:
На рисунке видно, что все уравнения баланса затрат выполняются, т.е. решение СЛАУ, а значит и стоимости всех хозяйственных операций найдены правильно!